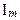Идеальные цепи переменного тока.
Рассмотрим участок цепи, состоящий из чистого активного сопротивления (рис. 1(а)). Вследствие действия переменной ЭДС по участку цепи протекает электрический ток i , равный:
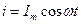 (11)
(11)
Так как участок однородный, то разность потенциалов на концах участка равна падению напряжения 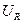 на этом участке. Согласно закону Ома:
на этом участке. Согласно закону Ома:
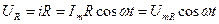 (12)
(12)
Видим, что амплитуда колебаний падения напряжения 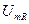 равна:
равна:
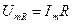 (13)
(13)
То есть находится по закону Ома. Колебания 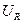 совершаются с той же частотой, что и колебания тока. Сдвиг фаз между колебаниями тока и падения напряжения равен нулю.
совершаются с той же частотой, что и колебания тока. Сдвиг фаз между колебаниями тока и падения напряжения равен нулю.
Соответствующая этому случаю векторная диаграмма изображена на рисунке 1(б).
 | |||
 | |||
б
а
Рис.1.
2) Рассмотрим цепь, состоящую из “чистой” индуктивности (рис. 2). В такой цепи возникает явление самоиндукции. Падение напряжения на этом участке равно:
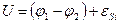 (14)
(14)
Здесь 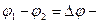 разность потенциалов на концах участка.
разность потенциалов на концах участка.
По закону Ома 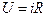 (R – активное сопротивление участка).
(R – активное сопротивление участка).
Так как для данного участка цепи R = 0, то U = 0 и и из уравнения (14) следует:
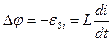 (15)
(15)
Если закон изменения силы тока определяется формулой (11), то
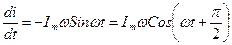
Подставляя это значение в уравнение (15) получим:
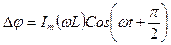
Из сравнения этого выражения с уравнением (12) следует, что индуктивность в цепи переменного тока эквивалентна активному сопротивлению 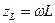 . Участок цепи при такой замене будет однородным, падение напряжения
. Участок цепи при такой замене будет однородным, падение напряжения 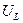 , будет равно разности потенциалов
, будет равно разности потенциалов 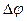 , то есть:
, то есть:
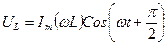 (16)
(16)
Амплитуда колебаний падения напряжения 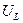 находится по формуле закона Ома
находится по формуле закона Ома
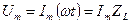 (17)
(17)
 Колебания
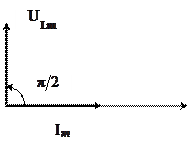
Колебания 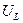 совершаются с той же циклической частотой, что и колебания тока, но опережают их по фазе на
совершаются с той же циклической частотой, что и колебания тока, но опережают их по фазе на 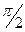 . Соответствующая этому случаю диаграмма изображена на рисунке 2(б).
. Соответствующая этому случаю диаграмма изображена на рисунке 2(б).

ось тока
|
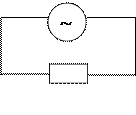
3) Рассмотрим идеализированную цепь, состоящую только из конденсатора, в которой активным сопротивлением и индуктивностью пренебрегаем (рис. 3(а)).
|
|
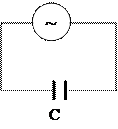

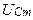
а б
Рис.3.
Разность потенциалов 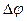 на концах такой цепи равна разности потенциалов на обкладках конденсатора.
на концах такой цепи равна разности потенциалов на обкладках конденсатора.
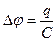 (18),
(18),
где q – заряд конденсатора, С – электроемкость конденсатора.
Так как сила тока 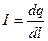 , то
, то 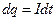 (19)
(19)
Значение заряда на обкладках конденсатора найдем интегрируя уравнение (19).
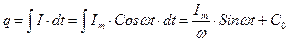
В полученном выражении 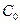 некоторая постоянная, представляющая собой постоянный заряд, накопленный конденсатором. Так как постоянный заряд в данном случае отсутствует, то
некоторая постоянная, представляющая собой постоянный заряд, накопленный конденсатором. Так как постоянный заряд в данном случае отсутствует, то 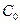 следует положить равной нулю. Тогда для q имеем
следует положить равной нулю. Тогда для q имеем
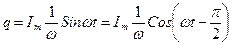 (20)
(20)
Подставляя это значение в уравнение (18) получим:
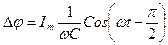 (21)
(21)
Сравнивая это выражение с (12) видим, что конденсатор в цепи переменного тока эквивалентен активному сопротивлению величиной 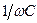 . При такой замене получаем однородный участок с сопротивлением
. При такой замене получаем однородный участок с сопротивлением 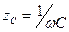 . Падение напряжения
. Падение напряжения 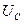 равно разности потенциалов
равно разности потенциалов 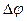 и равно
и равно
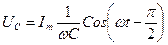 (22)
(22)
Амплитуда колебаний напряжения находится по формуле закона Ома.
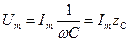 (23)
(23)
Из выражения (22) следует, что колебания 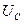 совершаются с той же циклической частотой, что и колебания тока, но отстают от них по фазе на
совершаются с той же циклической частотой, что и колебания тока, но отстают от них по фазе на 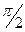 .
.
Соответствующая этому случаю, диаграмма изображена на рисунке 3(б).
9. Последовательная R,L,C – цепь.
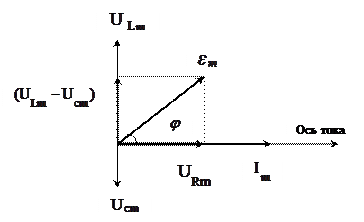 |

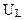
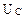
а б
Рис. 4.
Цепь представляет собой последовательно соединенные катушку с индуктивностью L, конденсатор емкостью С и активное сопротивление R. При таком соединение через все элементы протекает одинаковый ток, изменяющийся по закону
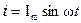
В соответствии с приведенным анализом каждый элемент рассматриваем как активное сопротивление с соответствующим значением падения напряжения. Тогда данное соединение представляет собой однородный участок цепи, на котором падение напряжения равно разности потенциалов на концах участка и равно сумме падений напряжения 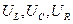 на каждом элементе. Так как между этими величинами имеет место сдвиг фаз, то амплитуду падения напряжения
на каждом элементе. Так как между этими величинами имеет место сдвиг фаз, то амплитуду падения напряжения 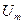 на всем участке, в соответствии с пунктом 3 §7, найдем из векторной диаграммы, представленной на рис. 4. На диаграмме произвольно выбрано
на всем участке, в соответствии с пунктом 3 §7, найдем из векторной диаграммы, представленной на рис. 4. На диаграмме произвольно выбрано 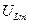 больше
больше 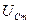 . Взаимное расположение векторов
. Взаимное расположение векторов 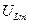 ,
, 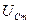 и
и 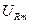 определяется сдвигом фаз между ними. Их значения найдем, применяя закон Ома к каждому из элементов
определяется сдвигом фаз между ними. Их значения найдем, применяя закон Ома к каждому из элементов
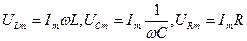 (24)
(24)
На диаграмме 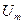 - гипотенуза прямоугольного треугольника катетами которого являются вектора
- гипотенуза прямоугольного треугольника катетами которого являются вектора 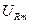 и
и 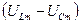 . Поэтому
. Поэтому
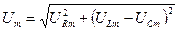
Подставляя сюда значения 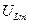 ,
, 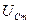 и
и 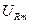 из (24) после несложных преобразований получим
из (24) после несложных преобразований получим
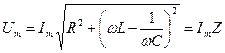 (25)
(25)
Данное выражение представляет собой закон Ома для рассматриваемого участка цепи, а
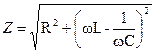 (26)
(26)
его полное сопротивление переменному току.
Сдвиг фаз между колебаниями тока падения напряжения, в соответствии с данной диаграммой, находится из уравнения 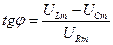 . Отсюда:
. Отсюда: 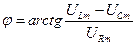 (27)
(27)
Подставляя сюда значения 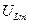 ,
, 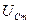 и
и 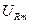 из уравнений (24) и , сокращая на
из уравнений (24) и , сокращая на 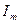 получим:
получим:
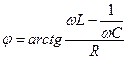 . (28)
. (28)
Мгновенное значение падения напряжения на рассматриваемом участке цепи будет определятся выражением:
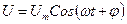 . (29)
. (29)
Дата добавления: 2015-03-07; просмотров: 2229;