Б) переменного прямоугольного сечения

Соотнесение.Пусть имеется два предмета. Требуется определить, относятся ли они к одному и тому же классу или различаются по весу. Ставим предметы на чаши весов (рис. а), делаем вывод. Для точного вывода здесь нет необходимости в шкалировании, поэтому весы «не нуждаются» ни в стрелке, ни в градуированной шкале.

Ранжирование.Имеем пять предметов. Их необходимо проранжировать строго по весу от наименьшего до наибольшего независимо от «конкретного» веса. Для этого на дуге наносятся метки в произвольном порядке (рис. б) и на оси весов закрепляется указатель (стрелка). Выбирается «на вид» наиболее легкий предмет и относительно него, ориентируясь по меткам на дуге, ранжируются остальные предметы. Если самый легкий предмет находится на левой чаше весов, то при последовательном соотнесении с ним остальных предметов стрелка будет отклоняться влево. Для решения задачи ранжирования не требуется числового градуирования меток дуги (нет необходимости в метрическом измерении).

Метрическое измерениетребует точного числового градуирования шкалы (рис. в), для чего используется эталон сравнения. В нашем случае таким эталоном может быть, например, гиря массой 1 кг, а градации шкалы наносятся, скажем, «по 10 г».

Отклонение стрелки при увеличении массы гирь на каждые 10 г обозначается на дуге «меткой» и числовым градуированием. Условная нулевая точка (точка равновесия) располагается в центре дуги. Построенную таким образом шкалу в дальнейшем можно использовать для измерения без помощи гирь.

Числовые значения измерения при помощи шкал в зависимости от используемого индикатора носят или дискретный (прерывный) характер, или непрерывный.

В первом случае говорят об экстенсивных величинах (например, численность имеющих определенный уровень образования, число членов семьи), во втором – об интенсивных (например, оценка респондентами просмотренного фильма по шкале «–1», «0», «+1», или «понравился», «никакого впечатления», «не понравился»).

Все оценочные суждения, высказываемые респондентами по поводу кого-то или чего-то, носят условно интенсивный характер. Это означает, что интервал между разными уровнями оценок является псевдоинтервалом и при операциях с числами не учитывается, как бы отсутствует, что позволяет назвать шкалы для измерения установок псевдонепрерывными. В естественных науках в качестве интенсивных используют шкалы-эталоны с нормированными числовыми величинами, например шкала температур, времени, т.е. измеряющие процесс. Числовые шкалы-эталоны, измеряющие статическое состояние (рост, вес, возраст, размер дохода и др.), имеют дело с дискретными величинами.

Математическая строгость измерения социальных явлений весьма условна, и здесь правильнее говорить о шкалировании. Это означает, что независимо от того, идет ли речь об экстенсивных или интенсивных величинах, первичным итогом измерения является классификация респондентов по позициям шкал. Без этой процедуры статистический анализ в социологии исключен.

Характер классификации респондентов предопределен используемыми шкалами. В процессе классификации осуществляются две процедуры:

1) структурирование объекта в соответствии со структурой предмета исследования, выявленной в результате операционализации (как бы перенос операциональной модели на объект – носитель социальной проблемы);

2) построение статистических рядов распределений, позволяющих применить для их анализа правила математической статистики.

В последнем случае правила, применимые для анализа тех или иных рядов распределений, предопределены видом используемой шкалы измерения.

Таким образом, на первой стадии измеряются свойства предмета исследования, для чего в качестве источника информации используется единица наблюдения (респондент, семья, группа). В результате мы имеем некоторые числовые значения, или символы (наименования), выступающие в качестве позиций шкал измерения. Классифицируя по этим значениям (или наименованиям) единицы наблюдения, получаем количества. Они всегда обозначаются рациональным числом, их содержания взаимно независимы, а структуры однозначны. Рассмотрим пример.

Относительно 100 респондентов есть две информации:

1) в их составе 60 женщин + 40 мужчин = 100 респондентов;

2) в их составе 60 респондентов намерены участвовать в выборах + 40 респондентов не намерены = 100 респондентов.

Независимо от различия в содержании информации в количественном отношении все числа равнозначны, в результате чего суммы в обоих случаях тождественны. Такое соответствие между величинами называют изоморфизмом.

Для измерения в социологии важен еще один аспект. Так как абсолютное большинство исследований носит выборочный характер, измерение происходит не на всем объекте, а лишь на его части – микромодели. Это рождает проблему соответствия измеренных на микромодели значений некоторых свойств их количественным параметрам в составе общей совокупности. Собственно количественные параметры здесь не могут совпадать хотя бы потому, что численность входящих в общую совокупность элементов многократно превышает численность элементов в микромодели. Речь может идти лишь об эквивалентности, совпадении структур микромодели и объекта по относительным (нормированным) числовым показателям свойств.

Например, если в микромодели из 100 человек 20 % в возрасте до 30 лет, 45 % – в возрасте 31–50 лет и 35 % в возрасте старше 50 лет и таково же процентное соотношение этих возрастных групп в общей совокупности, состоящей, скажем, из 10 000 человек, то между объектом и его микромоделью имеется гомоморфное соответствие (подобие). Такое соответствие крайне важно потому, что в прикладной социологии – это единственный критерий, позволяющий экстраполировать (переносить) результаты измерения свойств микромодели на всю совокупность.

Если на этапе социологического анкетирования происходит измерение, то на этапе классификации – простое исчисление, или объединение респондентов в однородные группы по единому признаку. Подобная процедура осуществляется многократно, в результате чего один и тот же респондент входит во множество групп, каждая из которых образована путем повторного соотнесения респондентов с позициями разных шкал. Именно тот факт, что в образованные по разным признакам классы входят одни и те же респонденты, гарантирует изоморфизм измерения независимо от того, что оно осуществлено на основании разнородных шкал.

Процесс измерения в социологии есть одновременно гомогенизация единиц наблюдения, их приведение к однородному виду (видам) на основании единого признака. Например, выделяя из состава всех жителей Российской Федерации часть совместно по двум критериям «только граждане страны» и только «в возрасте 18 лет и старше», мы получаем функционально однородную (независимо от пола, рода занятий, образования и т.д.) группу, называемую электоратом (избирателями).

Существует целый ряд проблем, связанных с практическим обеспечением того, чтобы измерение отвечало своей сути. Здесь в первую очередь следует назвать проблему взаимодействия объекта измерения и измерителя, «обратное воздействие», оказываемое на людей тестированием каких-то их личностных параметров. Так, известно, что на качество информации, получаемой от респондента, далеко не малое влияние оказывает поведение интервьюера. В то же время известно и не связанное с действием отдельных интервьюеров влияние опросов обществ, мнения на тот социум, из которого произведены соответствующие выборки.

Использованная литература:

1. Горшков М.К., Шереги Ф.Э. Прикладная социология: методология и методы: интерактивное учебное пособие. М.: Институт социологии РАН, 2011, 1 CD ROM.

2. Девятко И.Ф. Логика социологического исследования. М., 1987.

3. Осипов Г.В. Методы измерения в социологии / Г.В. Осипов, Э.П. Андреев. М., 1977.

4. Толстова Ю.Н. Измерение в социологии. М., 1998.

5. Шляпентох В.Э. Проблемы качества социологической информации: достоверность, репрезентативность, прогностический потенциал. М.: ЦСП, 2006. 664 с.

[1] Шляпентох В.Э. Проблемы качества социологической информации: достоверность, репрезентативность, прогностический потенциал. М.: ЦСП, 2006. 664 с. С. 61-62.

[2] Пфанцагль И. Теория измерений. М.: Мир, 1976. 248 с.

[3] Горшков М.К., Шереги Ф.Э. Прикладная социология: методология и методы: интерактивное учебное пособие. М.: Институт социологии РАН, 2011, 1 CD ROM

[4] Там же.

Рисунок 1 – Трехшарнирная рама

2) двухшарнирными жестко опертыми (такие рамы являются статически неопределимыми)

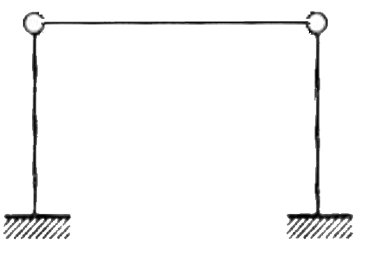
Рисунок 2 – Двухшарнирная жестко опертая рама

3) двухшарнирными шарнирно опертыми (тоже статически неопределимые)

Рисунок 3 – Двухшарнирная шарнирно опертая рама

Наиболее распространенными являются трехшарнирные рамы, т.к. в статически определимых системах не происходит перераспределения усилий при деформировании под длительно действующей нагрузкой, что обеспечивает соответствие их расчетным усилиям.

- По конструктивному решению различают:

1) рамы построечного изготовления;

2) рамы заводского изготовления.

Рамы построечного изготовления из досок и брусьев собирают непосредственно на строительной площадке. В этих рамах используются преимущественно податливые виды соединений: болты, гвозди, упоры.

Ригель и стойки таких рам могут иметь сплошное сечение или выполняются в виде решетчатых систем.

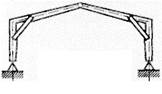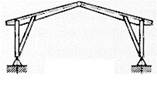а) б) в)

Рисунок 4 – Рамы построечного изготовления а) с подкосами в карнизном узле б) с опорными подкосами в) с решетчатыми стойками

К рамам построечного изготовления относятся также рамы с перекрестной стенкой на гвоздях. Конструкция таких рам аналогична конструкции балки с перекрестной стенкой на гвоздях.

Рамы построечного изготовления отличаются большим количеством узлов и требуют больших затрат труда и высококачественных материалов, поэтому наибольшее распространение получили рамы заводского изготовления или клееные рамы.

В зависимости от технологии изготовления или используемых материалов клееные рамы можно разделить на три группы:

1) гнутоклееные (из склеенных по пласти досок);

2) дощатоклееные из прямолинейных элементов;

3) клеефанерные, имеющие дощатые пояса и стенки из водостойкой фанеры.

Эти рамы, как правило, имеют прямолинейные элементы ригеля и стойки.

Распространенными конструкциями являются гнутоклееные рамы прямоугольного сечения, состоящие из гнутых, склеенных по пласти, досок.

Рисунок 5 – Гнутоклееная рама

В таких рамах для образования карнизного узла доски выгибаются, образуя плавный переход от ригеля к стойке. Таким образом, жесткий узел здесь выполняется цельноклееным, что выгодно отличает данную конструкцию от рам с карнизными узлами на податливых связях.

При наибольшей высоте стойки вся рама выполняется из двух элементов
Г-образного очертания, соединенных между собой в коньке.

Вместе с этим гнутоклееные рамы имеют существенные недостатки экономического порядка. В связи с необходимостью выгиба досок в узле сопряжения ригеля и стойки для этих рам необходим тонкий пиломатериал (δ=12…17 мм после острожки), что связано со значительным удорожанием конструкции: при использовании таких досок резко увеличиваются потери древесины и расход клея, а также трудозатраты на изготовление.

В результате оказывается, что гнутоклееные рамы являются по себестоимости, наиболее дорогие из всех рам.

Более эффективны рамы из прямолинейных элементов с жесткими клееными узлами: эти конструкции отвечают требованиям поточно-конвейерного производства, для их изготовления используется пиломатериал обычной толщины. При этом склеивают пакет досок, который затем распиливают по диагонали, получая при этом две сойки или два ригеля.

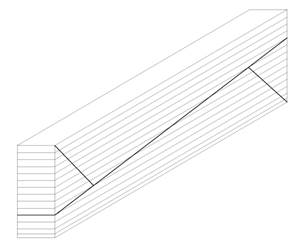
Рисунок 6 –Клееный пакет досок (заготовка для полурам)

Существует несколько конструктивных решений соединения прямолинейных элементов рам в жестком узле.

1. Ригель и стойка соединяются при помощи приклеенных к ним в узле двусторонних накладок из бакелизированной фанеры.

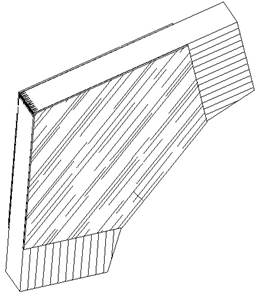
Рисунок 7 – Соединение ригеля и стойки накладками из фанеры

Рамы этого вида имеют несомненные технологические и экономические достоинства. Вместе с тем надежность узла на накладках из бакелизированной фанеры вызывает сомнения: в клеевых швах по плоскостям приклейке накладок к широким дощатым элементам могут возникнуть (при колебаниях влажности) опасные внутренние напряжения, обусловленные различием влажностных деформаций древесины и бакелизированной фанеры. Величину этих напряжений теоретически установить затруднительно, т.к. неизвестна действительная деформация клееного пакета.

Для окончательных выводов о надежности рам с фанерными накладками необходимы опытные данные, на основе которых и может быть решен вопрос о возможности массового применения таких конструкций.

2. Соединение ригеля со стойкой на зубчатый шип.

Это более надежный и перспективный тип соединения.

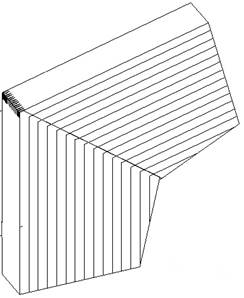
Рисунок 8 – Соединение ригеля со стойкой на зубчатый шип

Однако при таком соединении стойки и ригеля в карнизном узле возникают нежелательные концентрации напряжений, поэтому чаще сопряжения элементов рамы в жестком узле производят при помощи специальных вставок, соединенных с ригелем и стойкой.

3. Соединение ригеля со стойкой с помощью вставок. По форме вставки могут быть двух видов:

1) пятиугольные

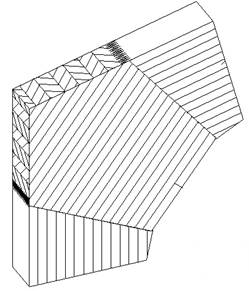
Рисунок 9 – Соединение ригеля и стойки при помощи пятиугольной вставки

2) гнутоклееные

а) 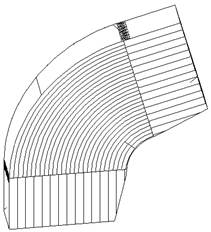б)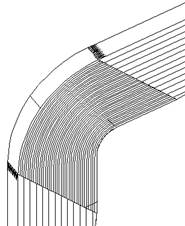

Рисунок 10 – Гнутоклееное соединение ригеля и стойки а) переменной длины б) постоянной длины

Первые (пятиугольные) вставки соединяются с элементами рамы под углом к волокнам. Поэтому в рамах с пятиугольными вставками определяющим условием при назначении размеров поперечного сечения элемента в узлах является несущая способность работающего под углом к волокнам на растяжение соединение его со вставкой.

Кроме этого, в самой вставке не исключается выклинивание кососрезных досок, выходящих на растянутую кромку рамы в месте наибольшего изгибающего момента.

Конструкции жестких узлов с такими вставками можно использовать только в легких рамах, где решающим фактором при назначении поперечных размеров элементов является расчет не по первому, а по второму предельному состоянию.

Более удачно решается жесткий рамный узел при помощи гнутоклееной вставки. Длина вставки вдоль рамы может быть либо постоянной (б), либо переменной (а). Вставки постоянной длины предпочтительнее, т. к. здесь увеличивается площадь клеевых швов в стыке, таким образом повышается надежность соединения.

Применение гнутоклееных вставок позволяет создавать рамные конструкции с широким диапазоном углов наклона ригеля к стойке.

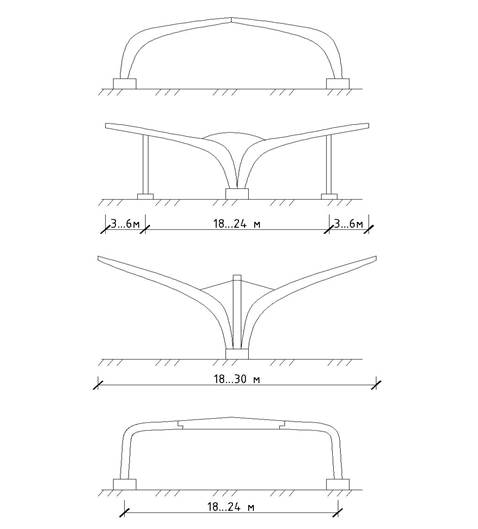
Рисунок 11 –Виды гнутоклееных рам

Существенную экономию пиломатериалов, облегчение веса и уменьшение стоимости конструкции можно получить в рамах, поперечное сечение которых состоит из дощатых поясов и фанерных стенок.

Клеефанерные рамы легче гнутоклееных на 35…40 %.

Поперечное сечение рам может быть двутавровым или двутаврово-коробчатым.

При выборе формы сечения элементов рам предпочтение следует отдавать поперечному сечению, состоящему из двух или нескольких склеенных по ширине двутавров. В этом случае обеспечивается симметричное загружение стенок сдвигающими усилиями относительно их продольных осей, а также увеличение количества площадок скалывания при проверке на скалывание между слоями шпона фанеры.

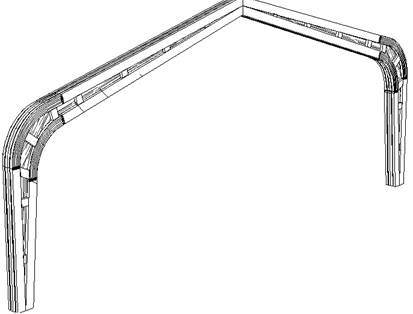
Рисунок 12 – Клеефанерная рама

Для стенок рекомендуется использовать фанеру марки ФСФ, как наиболее доступную по стоимости. Количество фанерных стенок, а так же их толщина определяются расчетом.

Сопряжение поясов (сжатого и растянутого) в жестком переломленном узле рамы рекомендуется проектировать с использованием гнутоклееных вставок, соединенных с дощатыми поясами рам зубчато-шиповым стыком.

В клеефанерных рамах указанные стыки могут размещаться как в одном сечении пояса, так и вразбежку. В последнем случае достигается увеличение надежности стыкуемого соединения.

Гнутоклееные вставки (внутренняя и наружная) могут изготавливаться из разных материалов: внутренняя, имеющая меньший радиус – из шпона, наружная – из досок.

Конструктивные возможности при создании разнообразных форм в клеефанерных рамах с гнутоклееными вставками больше, чем в клеедощатых: легко конструируются рамы с консолями, причем увеличение сечения в защемленных стойках достигается без перерасхода материалов, что позволяет создавать оригинальные по архитектурному решению здания.

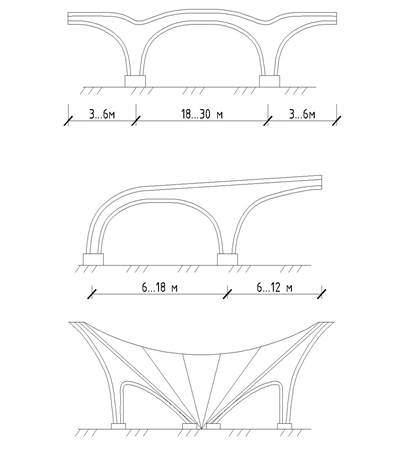
Рисунок 13 .Виды клеефанерных рам

Геометрические размеры клееных рам

Пролеты: 12…24 м,

Высота стоек: 2.6…4.5 м,

Уклон ригеля: 1/4…1/3,

Шаг: 3…6 м.

Высота сечения в коньке – не менее 0.3 высоты сечения в карнизном узле

Высота сечения в карнизном узле: 1/12… 1/30 пролета

Высота сечения стоек у опор: не менее 0.4 высоты в карнизном узле.

Расчету рамы предшествует установление ее расчетной схемы (двухшарнирная или трехшарнирная) и расчетной оси.

Расчет рамы выполняют в следующей последовательности:

1) статический расчет, т. е. вычисление усилий в элементах рамы от действия внешних нагрузок (снег, ветер) собственного веса рамы и веса покрытия;

2) проверка сечений рамы;

3) расчет узлов рамы.

При статическом расчете определяют усилия и строят эпюры М, N, Q от действия равномерно распределенной нагрузки отдельно от собственного веса конструкций, от снеговой нагрузки слева, справа от конькового узла и на всем пролете, а так же от действия равномерно распределенной нагрузки от ветра слева и справа.

При высоте стойки до 4 м расчет на ветровую нагрузку можно не производить.

Например, так выглядит загружение от собственного веса.

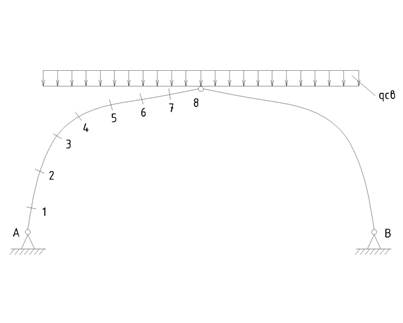
Рисунок 14 – Загружение рамы от собственного веса

Усилия в раме можно определять либо относительно ее геометрической оси, либо относительно наружного контура. В последнем случае необходима корректировка изгибающего момента вследствие переноса нормальной силы с нагруженного контура на ось сечения.

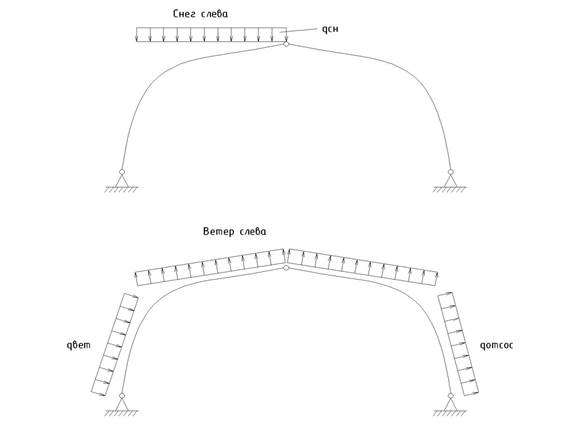
Рисунок 15 – Варианты загружения рам

Усилия определяются методами строительной механики в характерных точках по периметру рамы, например А, 1, 2, 3, 4, 5, 6, 7, 8. Количество точек определяется характером эпюр.

Для примера покажем эпюры M, N, Q от равномерно распределенной нагрузки слева от конькового узла.

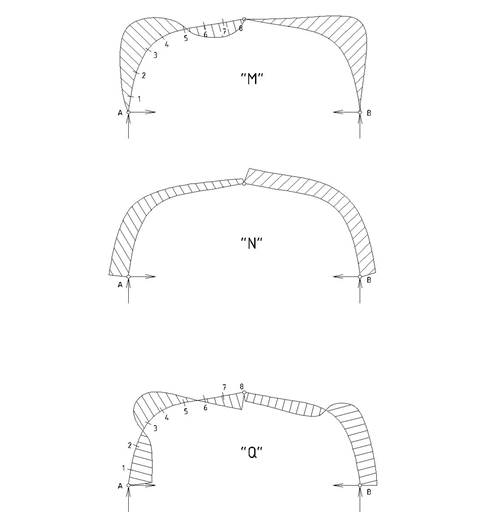
Рисунок 16 – Эпюры M, N и Q

Целесообразно сначала определить усилия и эпюры от равномерно распределенной единичной нагрузки (q₁=1), а затем с учетом коэффициента k=q/q₁, (где q – реальная нагрузка, q₁ – единичная нагрузка) определять усилия от реальных нагрузок.

В результате статического расчета определяются расчетные усилия в сечениях рамы при основных и дополнительных сочетаниях нагрузок:

а) расчетная постоянная и временная на всем пролете;

б) постоянная на всем пролете, временная – на половине пролета;

в) по схемам а и б в сочетании с ветром.

При выполнении статического расчета рамы, также как и при расчете других конструкций необходимо пользоваться СНиП «Нагрузки и воздействия».

Поскольку в настоящее время в практике строительства применяют только клееные рамы, то в дальнейшем речь будет идти об этих рамах.

Проверка сечений рамы

Наиболее напряженными сечениями по нормальным напряжениям, если обратить внимание на эпюры M и N, для рам являются карнизные узлы, а для рам с подкосами – сечения у концов подкоса в местах примыкания его к стойке и ригелю.

1. Расчет на прочность элементов трехшарнирных рам в их плоскости допускается выполнять по правилам расчета сжато-изгибаемых элементов с расчетной длиной, равной длине полурамы по осевой линии:

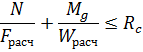
2. Устойчивость плоской формы деформирования трехшарнирных рам допускается выполнять по формуле:

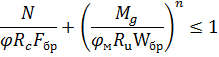
Криволинейные участки гнутоклееных рам

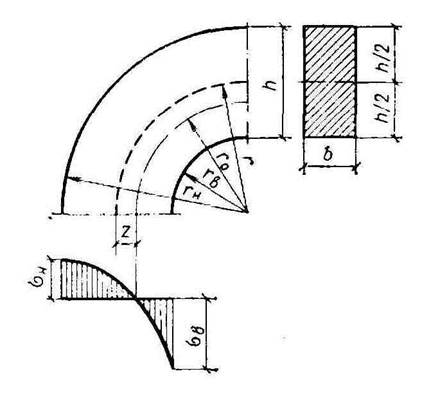
Рисунок 17 – Криволинейный участок гнутоклееной рамы

Криволинейные участки гнутоклееных рам при отношении h/r≥1/7 (h – высота сечения, r – радиус кривизны центральной оси криволинейного участка) следует рассчитывать

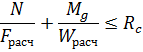
Здесь при проверке напряжений по внутренней кромке расчетный момент сопротивления следует умножать на коэффициент k_rb:

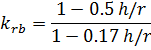
Расчет узлов рамы

Для рам заводского изготовления выполняется расчет опорного и конькового узлов. Опорные шарнирные узлы клееных рам могут быть весьма разнообразными.

Покажем несколько вариантов опорных узлов:

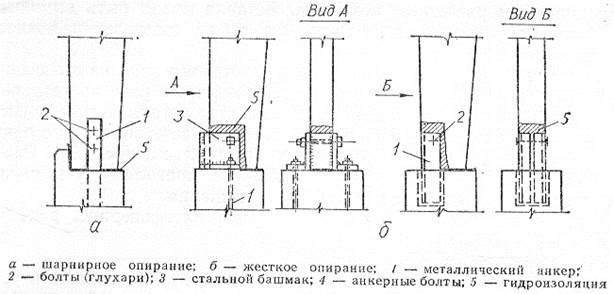
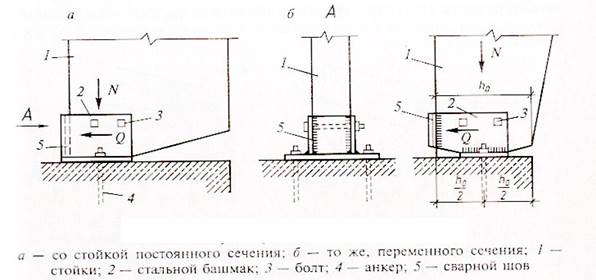
Рисунок 18 – Варианты опорных узлов

Для всех вариантов опорных узлов продольная сжимающая сила N воспринимается смятием вдоль волокон древесины стойки. В этом случае проверку выполняют по формуле:

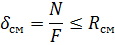
Поперечная сила Q может быть передана на фундамент через болты или глухари, крепящие стойку к стальным элементам, заделанным в фундамент. В этом случае рассчитывается количество болтов, воспринимающих силу Q.

В другом варианте опорного узла поперечная сила передается через деревянный брусок или через вертикальный лист стального башмака. В этом случае

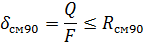
Коньковый узел чаще всего решается с деревянными накладками на болтах, хотя возможны и другие варианты конькового узла (при больших величинах поперечной силы), например, с металлическими соединительными деталями.

Рисунок 19 – Коньковый узел

Количество болтов рассчитывается из условия восприятия ими поперечной силы.

Лобовые упоры соединения ригелей рассчитывают на смятие под углом и вдоль волокон на действие продольной силы N.

Рисунок 1 - Дощатоклееные стойки

а) постоянного прямоугольного и квадратного сечения;

б) переменного прямоугольного сечения

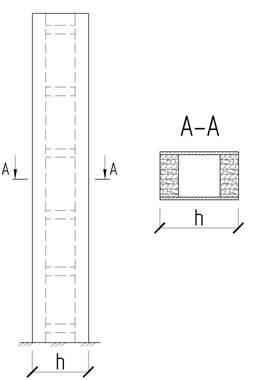
Рисунок 2 - Клеефанерные стойки

Клееные стойки могут иметь больше поперечное сечение и высоту до 8-10 м. Для их изготовления используют древесину 2 и 3 сортов. Достоинства таких стоек состоят в их индустриальности, простоте транспортирования и монтажа.

Стойки из цельных элементов

Подразделяются на следующие виды:

1) в виде одиночного бруса или бревна

Рисунок 3 - Стойки из одиночных бревен и брусьев

Такие стойки обладают сравнительно небольшой несущей способностью. Их высота и размер поперечного сечения ограничено сортаментом лесоматериалов.

В этих стойках применяют обычно шарнирное опирание на фундамент.

2) Стойки в виде элементов составного сечения набранного из двух или нескольких брусьев, досок или бревен, соединенных болтами или другими податливыми связями

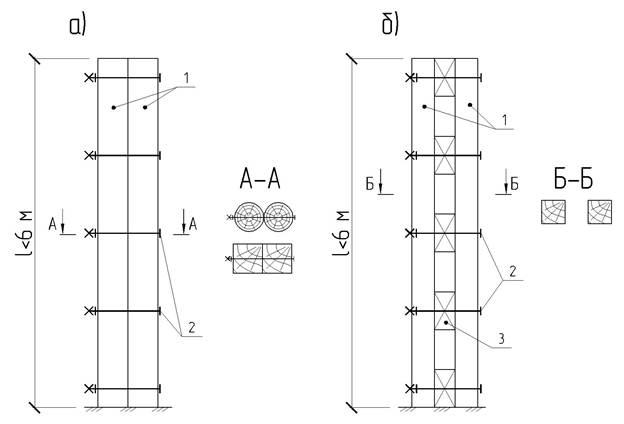
Рисунок 4 – Составные брусчатые стойки