Связь теории функций комплексного переменного с плоской задачей теории фильтрации. Функция тока. Комплексный потенциал

Плоское движение несжимаемой жидкости в пористой среде, следующее линейному закону фильтрации, является наиболее хо­рошо исследованным благодаря тому обстоятельству, что здесь ока­залось возможным применить одно из наиболее мощных средств ма­тематического анализа — аппарат теории функций комплексного переменного.

Рассмотрим плоское движение несжимаемой жидкости в пористой среде. В этом случае мы имеем следующие уравнения движения:

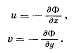
(3.1)

Проекция скорости на ось 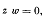потенциал 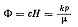зависит только от координат х и у.

Уравнение неразрывности для несжимаемой жидкости прини­мает вид:

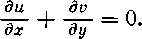(3.2)

Подставляя значения компонент скорости u, v из уравнений (3.1) в уравнение неразрывности (3.2), получаем уравне­ние Лапласа на плоскости

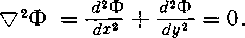(3.3)

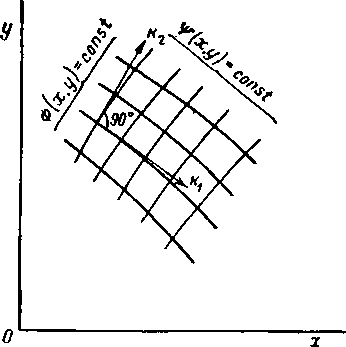
Найдем уравнение линий тока нашего плоского движения.

Напомним определение линии тока. Линия тока — это линия, касательная к которой в любой точке совпадает по направлению с вектором скорости жидкости частицы, находящейся в этой же точке.

Можно построить новую функцию, связанную определенным обра­зом с потенциалом скоростей. Эта новая функция, называемая функ­цией тока, даст нам представление о всей картине движения. К со­жалению, такую функцию удается ввести только для плоского или осесимметричного движения. Для пространственного трехразмер­ного движения такой функции ввести не удается, и поэтому простран­ственное движение изучено гораздо хуже, чем плоское.

Дифференциальное уравнение линии тока устанавливается как следствие определения этой линии. В общем случае движения направ­ляющие косинусы касательной к линии тока равны косинусам углов, которые составляет с этими осями вектор скорости V. Отсюда следует

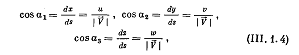
(3.4)

где ds — элемент линии тока с проекциями 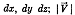— модуль вектора скорости. Для плоского движения остаются два уравнения:

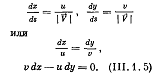
(3.5)

Будем искать интеграл этого дифференциального уравнения в виде неявной зависимости

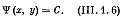
(3.6)

Меняя постоянную С, по­лучаем уравнение семейства линий тока. Изменение С со­ответствует переходу от од­ной линии тока к другой (рис.3.1).

Введенная нами функция Ѱ= Ѱ (х,у) обладает тем свойством, что она постоянна не во всех точках плоскости, а только вдоль заданной линии тока. При переходе к другой линии тока константа С меняется. Функция Ѱ (х,у) называется функцией тока.

Найдем связь функции тока с потенциалом скорости Ф = Ф (х, у). Вдоль линии тока Ѱ (х,у) = const. Следовательно, полный диф­ференциал функции тока определяется уравнением

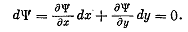
(3.7)

Уравнения (3.5) и (3.7), очевидно, совпадают. Таким образом,

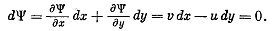
(3.8)

Сравнивая в уравнении (3.8) коэффициенты при dx и dy,

получаем

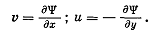
(3.9)

Сравним проекции скоростей и и v из системы (3.9) с проекциями скоростей из основной системы (3.1). Получаем

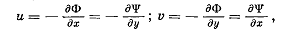
отсюда

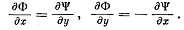(3.10)

Уравнения (3.10) называются обычно уравнениями Коши и Римана.

Докажем, что Ѱ (х,у) удовлетворяет уравнению Лапласа.

Из системы (3.10), дифференцируя первое уравнение по у, вто­рое по х, получаем

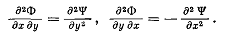
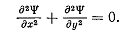Вычитая второе уравнение из первого, получаем

(3.11)

Уравнения (3.10) имеют связь с теорией функций ком­плексного переменного.

Введем комплексное переменное. Пусть плоскость течения при­нята за плоскость комплексного переменного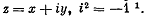

Аналогично тому, как составлено комплексное переменное z = x + iy, составим новую комплексную функцию Ф (x, у) + i Ѱ (x, у).

Возникает следующий вопрос: можно или нельзя представить эту функцию в виде некоторой функции комплексного переменного F(z) = F(x + iy)?

Не всякая комплексная функцияМ (x, у) + iN (x, у), где М (x, у), N (х, у) — произвольные функции двух переменных ж и у, будет функцией комплексного переменного z = x + iy. В том, что это так, можно убедиться на очень простом примере.

Возьмем функцию F (z) = z² = (x - i 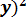- Раскрывая квадрат сум­мы, получаем

F (z) = z² = x² - у² + 2xy.

Таким образом, если взять две функции

М (x, у) = x² — у², N (x, у) = 2xу,

затем составить комплексную функцию M(x, у) + iN (x, у) = = x² — у² + i2xу, то в данном случае мы «экспериментально» убе­димся, что эта функция x² — y² + i2xу действительно является функцией комплексного переменного z = x + iу.

А теперь возьмем и «испортим» какую-либо из этих функций, например, положим М₁ (x, у) = x² + у².

Если составить теперь функцию 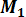(x, у) + iN (x, у) = x² + у² + i2xу, где одна из этих функций «испорчена», то такой комп­лекс уже не будет функцией комплексного переменного z= x+ iy.

Оказывается, что уравнения (3.10) являются необходимым и достаточным условием для того, чтобы комплексную функцию Ф (x, у) + i Ѱ (x, у) (где Ф — потенциал скорости; Ѱ — функция тока) можно было рассматривать как функцию комплексного пе­ременного z = x + iу.

Важность этого обстоятельства заключается в том, что функ­ции, зависящие от двух переменных ж и у, заменяются функцией, зависящей формально от одного переменного z = x +iy.

Чтобы доказать, что Ф +iѰ является не просто комплексом, а функцией комплексного переменного, обратимся к уравнениям Коши — Римана (3.10). При этом будем рассуждать так: если Ф + iѰ является функцией комплексного переменного z = x +iy,

Ф(x, у) + Ѱ (x, y) = F(z), (3.12)

то, следовательно, производная 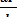должна иметь одно и то же

значение независимо от закона стремления 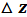→ 0.

Имея это в виду, продифференцируем уравнение (3.12) по ж. Учитывая правило дифференцирования сложных функций (а также, что z = х + iy), получаем:

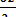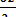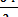= 1, = i,

+i 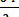= 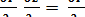(3.13)

Продифференцируем теперь уравнение (3.12) по у

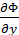+ i = .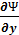

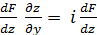Разделив последнее уравнение на i, получим

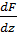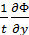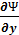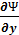= + = -i 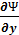(3.14)

Таким образом, из уравнений (3.13) и (3.14) следует

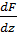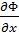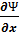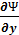= + i = -i 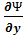(3.15)

Сравнивая в уравнении (3.15) действительную и мнимую части, получаем уравнения Коши — Римана

= , =

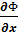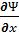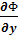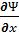
полностью совпадающие с уравнениями (3.10).

Следовательно, если взять любую функцию комплексного пе­ременного

F(z)=F(x + iy)

и отделить в ней действительную часть Re F(z) от мнимой 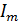F 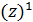, то можно трактовать действительную часть, как потенциал неко­торого плоского фильтрационного потока, мнимую часть — как функ­цию тока этого течения:

Re F(z) = Ф(х, у), Im F(z) = 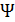(х, у).

Приравнивая действительную часть постоянной величине, по­лучаем семейство эквипотенциалей:

Ф(х, у) = const.

Приравнивая мнимую часть другой константе, получаем семей­ство линий тока 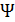(х, у) = const

Таким образом, каждой функции комплексного переменного можно сопоставить некоторый плоский фильтрационный поток. Зная функцию комплексного переменного F (z) = Ф (х, у) + i 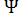(х, у), z = х + iy, называемую характеристической функцией течения или комплексным потенциалом, сразу получаем всю картину движения: семейство эквипотенциалей, семейство линий тока и поле скоростей.

Теория функций комплексного переменного в настоящее время имеет широчайшее применение в гидродинамике, аэродинамике, теории фильтрации, теории упругости, теории электричества и теп­лоты и т. д.

Докажем, что линии тока и эквипотенциальные линии образуют ортогональную сетку, т. е. каждая пара кривых этих двух семейств пересекается под прямым углом (рис.3.1).

Уравнения эквидотенциалей и линий тока имеют вид:

Ф (х, у) = const, 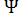(х, у) = const, (3.16)

Отсюда

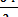dx + 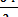dy = 0, 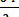dx + 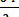dy = 0 (3.17)

Угловой коэффициент 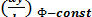= 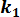касательной к эквипотенциали

определяется из первого уравнения (3.17):

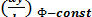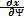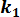= - = (3.18)

Совершенно аналогично найдется из второго уравнения (3.17) и угловой коэффициент k₂ касательной к линии тока:

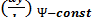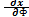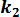
= - = (3.19)

Из уравнений Коши — Римана следует, что 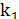k₂ = — 1. Дей­ствительно. учитывая (3.10), получаем

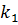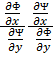k₂= = -1,

что (как известно из аналитической геометрии) имеет место для прямых, пересекающихся под прямым углом. Таким образом, линии тока будут пересекать эквипотенциали под прямым углом.