Движение жидкости в пласте от источника к стоку.

Случай двух скважин — нагнетательной и эксплуатационной. Для простоты разместим их вдоль оси х. Пусть в точке х = а, у = 0 находится скважина-сток, в точке х = — а, у — 0 — скважина-источник. Найдем потенциал движения, образованного совместной работой двух скважин. Потенциал и функция тока для первой скважины (опуская постоянные слагаемые) будут равны

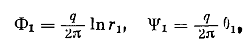(5.1)

где r¹ — расстояние от точки М, где определяется потенциал, до первой скважины; б_х — угол, составляемый радиусом-вектором r₂ с осью х.

Совершенно аналогично для второй скважины (также опуская константу) получим

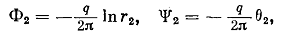
где г₂ — расстояние от точки М до второй скважины; б₂ — угол, составленный г₂ с осью х.

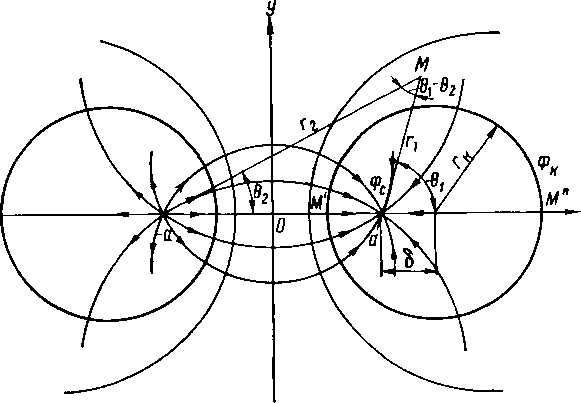Течение при равнодебитных стоке и источнике на плоскости.

Добавляя произвольную постоянную С, получаем выражение комплексного потенциала результирующего течения в виде

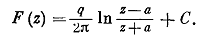
Докажем, что линии тока будут окружностями, выходящими из нагнетательной скважины и заканчивающимися в эксплуатационной. Найдем потенциал и функцию тока результирующего движения:

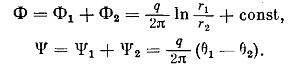
А*ln(r₁/r₂)=kP/µ+C => P=(qµ)/(2πk)*ln(r₁/r₂)+C

Рассмотрим 2 случая

1)P=P_c, r₁=r_c, r₂=2a

2) P=P_н, r₂=r_c, r₁=2a

В итоге получим дебит:

<7 8 91011 12 13 >

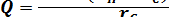
Дата добавления: 2015-02-10; просмотров: 1637;