Определение дебита скважины в пласте с круговым контуром питания.
Пусть центры скважин располагаются в вершинах правильного n-угольника, т.к. что скважины образуют кольцевую батарею радиуса а (рис.8.1). Контур питания удалён от скважин на расстояние, значительно превышающее радиус батареи, и тогда можно считать, что все скважины равноудалены от контура питания на расстояние rк. Будем считать, что на контуре питания поддерживается постоянное значение потенциала jк и на контуре скважин потенциал постоянен и равен jс. В данной постановке, следовательно, надо решить задачу о плоском течении к n точечным стокам, размещённым равномерно на окружности радиуса а.
Рис. 8.1. Схема кольцевой батареи
|
Для получения формулы дебита скважин воспользуемся формулой (7.2):
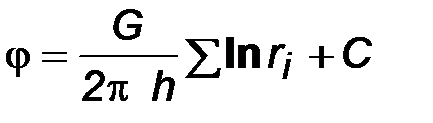, (8.1) (7.15)
где G - массовый дебит любой скважины батареи, rj - расстояния от некоторой точки пласта до всех n скважин; h - толщина пласта.
Граничные условия:
на контуре питания j=jк=const,при rj=rк;
на контуре скважины j=jс=const, при r1=rс; rj(j¹1)=2a sin[(n-1)p/n].
Используя данные граничные условия, преобразуем формулу (8.1):
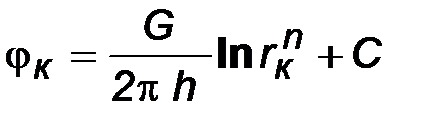, (8.2)
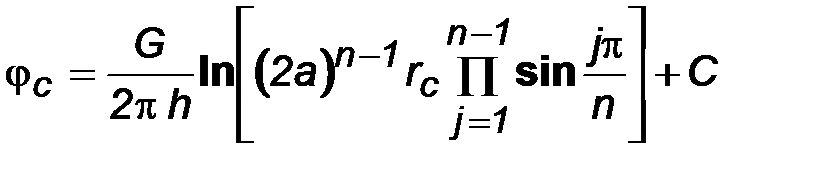. (8.3)
В последнем выражении
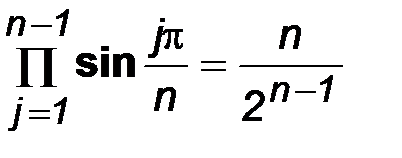. (8.4)
Тогда (8.3) перепишется в виде
(8.5)
и из (8.2), (8.5) получим выражение для определения дебита скважины
.
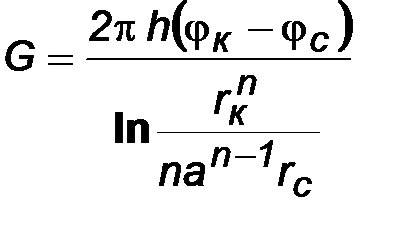Дата добавления: 2015-02-10; просмотров: 2141;