Задачи, решаемые на плоскости функции комплексного переменного.
Функция 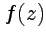 называется аналитической в некоторой области
называется аналитической в некоторой области 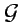 , если она дифференцируема в этой области, а ее производная непрерывна. Из определения и свойств производных, рассмотренных выше, следует, что необходимым и достаточным условием аналитичности функции
, если она дифференцируема в этой области, а ее производная непрерывна. Из определения и свойств производных, рассмотренных выше, следует, что необходимым и достаточным условием аналитичности функции 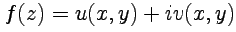 является непрерывность частных производных функций
является непрерывность частных производных функций 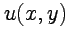 и
и 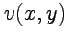 , которые также должны подчиняться условиям Коши-Римана
, которые также должны подчиняться условиям Коши-Римана 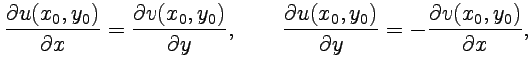
(4.1)
Из определения следуют свойства аналитических функций, которые часто полезно использовать при решении задач:
если функция является аналитической в области 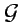 , то она непрерывна в этой области;
, то она непрерывна в этой области;
если 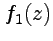 и
и 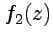 - аналитические функции в области
- аналитические функции в области 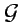 , то их сумма и произведение также являются аналитическими в области
, то их сумма и произведение также являются аналитическими в области 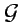 , а функция
, а функция 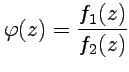 является аналитической всюду, где
является аналитической всюду, где 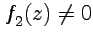 ;
;
если 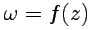 является аналитической в области
является аналитической в области 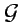 комплексной плоскости
комплексной плоскости 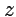 , а в области ее значений
, а в области ее значений 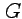 определена аналитическая функция
определена аналитическая функция 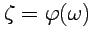 , то функция
, то функция 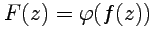 является аналитической функцией в области
является аналитической функцией в области 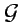 ;
;
если 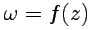 является аналитической функцией в области
является аналитической функцией в области 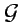 и
и 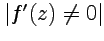 в окрестности некоторой точки
в окрестности некоторой точки 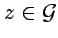 , то в окрестности точки
, то в окрестности точки 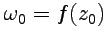 области
области 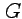 значений
значений 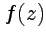 определена обратная функция комплексной переменной
определена обратная функция комплексной переменной 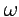 ,
, 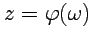 , которая является аналитической и имеет место формула
, которая является аналитической и имеет место формула
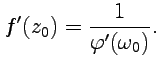
Пример 1. Найти постоянные 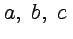 , при которых функция
, при которых функция 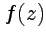 будет аналитической, и вычислить производную
будет аналитической, и вычислить производную 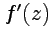 :
:
1. 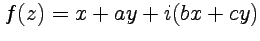 ;
;
2. 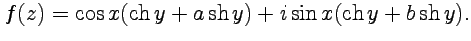
Решение. Значения постоянных можно найти из требования выполнения условий Коши-Римана.
1. Так как 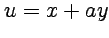 ,
, 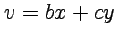 , то вычисляя призводные в (4.1), получим
, то вычисляя призводные в (4.1), получим

| (4.2) |
Таким образом, остается одна произвольная константа 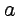 (или
(или 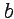 ) и при условии (2) аналитическая функция
) и при условии (2) аналитическая функция 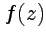 запишется в виде:
запишется в виде:
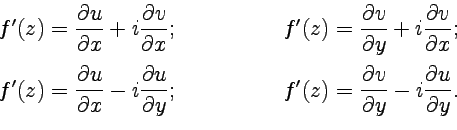
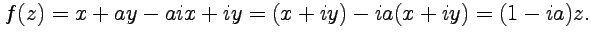
Производную можно найти, пользуясь формулами:
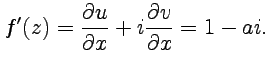
(4.3)
2. Аналогично, вычисляя частные производные функций и сравнивая результаты, получим
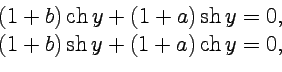
и, так как функции 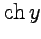 и
и 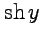 являются линейно независимыми, то
являются линейно независимыми, то
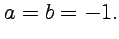
Подставляя полученные значения постоянных в определение функции и используя формулу Эйлера, имеем
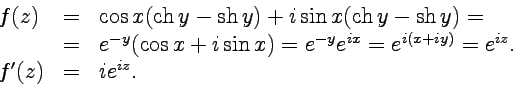
Рассмотренные примеры являются частными случаями общего свойства, согласно которому правила дифференцирования функций действительной переменной являются справедливыми и для аналитических функций.
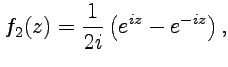
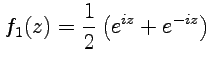 Пример 2. Показать, что функции, определенные соотношениями:
Пример 2. Показать, что функции, определенные соотношениями:
1) 2)
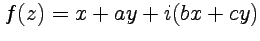 являются аналитическими на всей комплексной плоскости, и вычислить их производные.
являются аналитическими на всей комплексной плоскости, и вычислить их производные.
Решение. В примере 1)
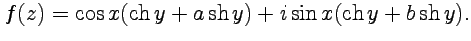 2)
2)
показано, что функция 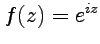 является аналитической, тогда на основании свойств аналитических функций (сумма и частное), перечисленных выше, сразу можно получить утверждение задачи, и, пользуясь эквивалентностью правил дифференцирования аналитических функций, получить выражения для производных в следующем виде:
является аналитической, тогда на основании свойств аналитических функций (сумма и частное), перечисленных выше, сразу можно получить утверждение задачи, и, пользуясь эквивалентностью правил дифференцирования аналитических функций, получить выражения для производных в следующем виде:
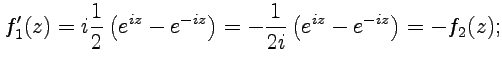
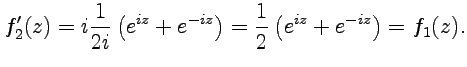
Кроме того, прямым вычислением можно получить следующее тождество для функций 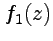 и
и 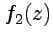 :
:
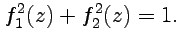
Таким образом 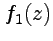 ,
, 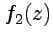 подчиняются известным свойствам тригонометрических функций, а для
подчиняются известным свойствам тригонометрических функций, а для 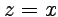 просто совпадают с ними:
просто совпадают с ними: 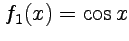 ,
, 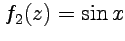 . Поэтому естественным будет сохранить и для функций комплексной переменной те же обозначения и, таким образом, расширить определение тригонометрических функций на множество комплексных чисел:
. Поэтому естественным будет сохранить и для функций комплексной переменной те же обозначения и, таким образом, расширить определение тригонометрических функций на множество комплексных чисел:
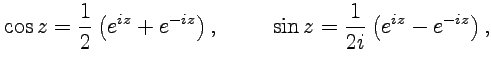
| (4.4) |
и также для гиперболических функций:
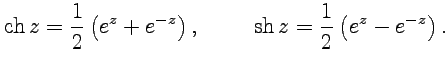
| (4.5) |
Пример 3. Показать, что для аналитических функций имеет место соотношение
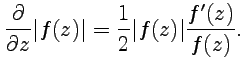
| (4.6) |
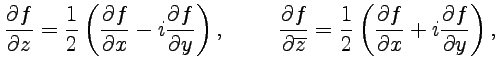 Решение. Вычислим формальную производную на основе определения :
Решение. Вычислим формальную производную на основе определения :
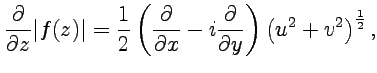
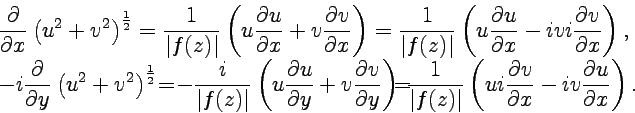
Тогда
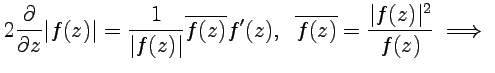
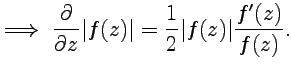
Формальное вычисление:
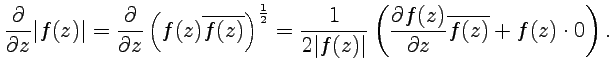
Так как 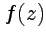 является аналитической функцией, то
является аналитической функцией, то 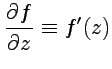 , что приводит к такому же результату.
, что приводит к такому же результату.
Пример 4. Найти производные 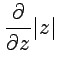 и
и 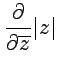 .
.
Решение. Применение формулы (6) для функции 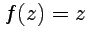 с учетом значения производной
с учетом значения производной 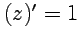 дает:
дает:
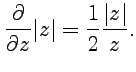
Аналогично, используя определения
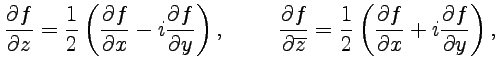
и учитывая, что 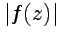 - действительная функция, получим
- действительная функция, получим
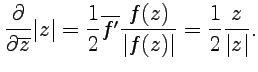
Дата добавления: 2015-02-10; просмотров: 3654;
