Представление об источниках и стоках на плоскости и в пространстве

Назовем точечным стоком на плоскости точку, поглощающую жидкость. Сток можно рассматривать как гидродинамически совершенную скважину бесконечно малого радиуса в пласте единичной толщины. На плоскости вокруг точечного стока будет радиальная картина движения. Точечный источник - это точка, выделяющая жидкость (модель нагнетательной скважины). Определим потенциал течения как функцию, производная которой с обратным знаком вдоль линии тока равна скорости фильтрации, т. е.

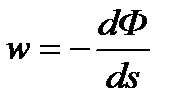(2.1)

Из сравнения (2.1) с законом Дарси:

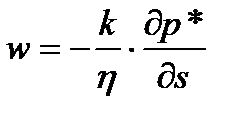
видно, что потенциал для несжимаемой жидкости связан с давлением формулой

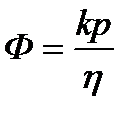(2.2)

Найдем потенциал точечного стока на плоскости. Так как точечный сток является моделью добывающей скважины и течение вокруг него плоскорадиальное, то можно воспользоваться формулой объемной скорости 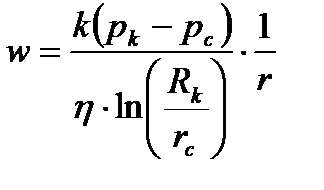, то

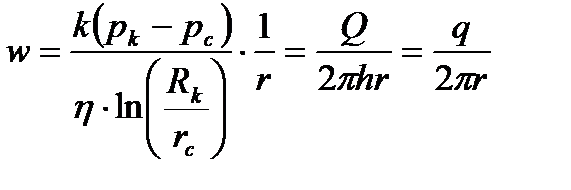(2.3)

где 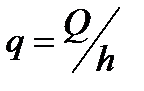- дебит скважины-стока, приходящийся на единицу толщины пласта.

Но для плоскорадиального потока:

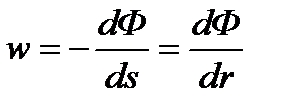
Откуда

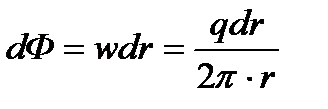
Проинтегрировав получим выражение потенциала для точечного стока на плоскости:

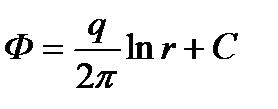(2.4)

где С - постоянная интегрирования.

Таким образом, потенциал в окрестности скважины-стока пропорционален логарифму расстояния г от стока (центра скважины). При r = 0 и r= 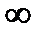, то функция ln r обращается в бесконечность, поэтому потенциал в этих точках теряет смысл.

Для точечного источника справедливы все приведенные формулы, но дебит q считается отрицательным (q < 0).

Из формулы (2.4) следует, что линиями равного потенциала (эквипотенциалами) являются окружности r = const.

Найдем теперь потенциал точечного стока в пространстве. Движение вблизи такого стока будет радиально-сферическим. Поэтому скорость фильтрации

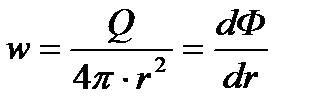
Откуда

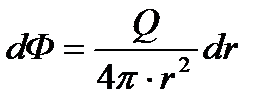
и потенциал точечного стока в пространстве будет иметь вид:

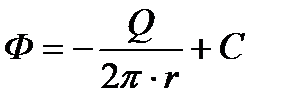(2.5)

Для потенциала точечного источника знак дебита в формуле (2.5) меняется на противоположный.

Как следует из формулы (2.5), потенциал точечного стока в пространстве обращается в бесконечность при r = 0, а при r = 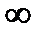остается конечным (и равным С).

Распределение давления и потенциала в установившихся потоках несжимаемой жидкости описывается уравнением Лапласа, которое для плоских течений имеет вид

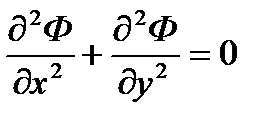(2.6)

Поскольку уравнение Лапласа линейное и однородное, его решения обладают следующими свойствами: сумма частных решений есть также решение этого уравнения; произведение частного решения на произвольную постоянную есть также решение этого уравнения. На основании этих свойств в подземной гидромеханике разработан метод решения сложных задач, названный методом суперпозиции (методом наложения решений).

Математический смысл метода суперпозиции заключается в том, что если имеется несколько фильтрационных потоков с потенциалами Ф1(х,у), Ф2(х, у},...,Фn(х, у), каждый из которых удовлетворяет уравнению Лапласа, т. е.

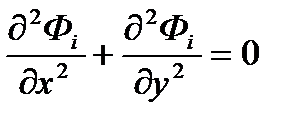. i =1,2,…,n

то и сумма 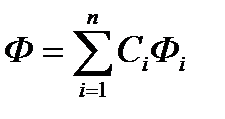(где С_i - произвольные постоянные) также удовлетворяет уравнению Лапласа:

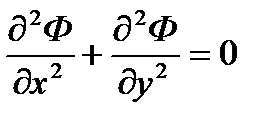
Гидродинамический смысл метода суперпозиции состоит в том, что изменение пластового давления и потенциала в любой точке пласта, вызванное работой каждой скважины (нагнетательной или добывающей), подсчитывается так, как если бы данная скважина работала в пласте одна, совершенно независимо от других скважин, затем эти независимо определенные для каждой скважины изменения давления и потенциала в каждой точке пласта алгебраически суммируются.

Суммарная скорость фильтрации находится как сумма векторов скоростей фильтрации, вызванных работой каждой скважины, по правилам сложения векторов.

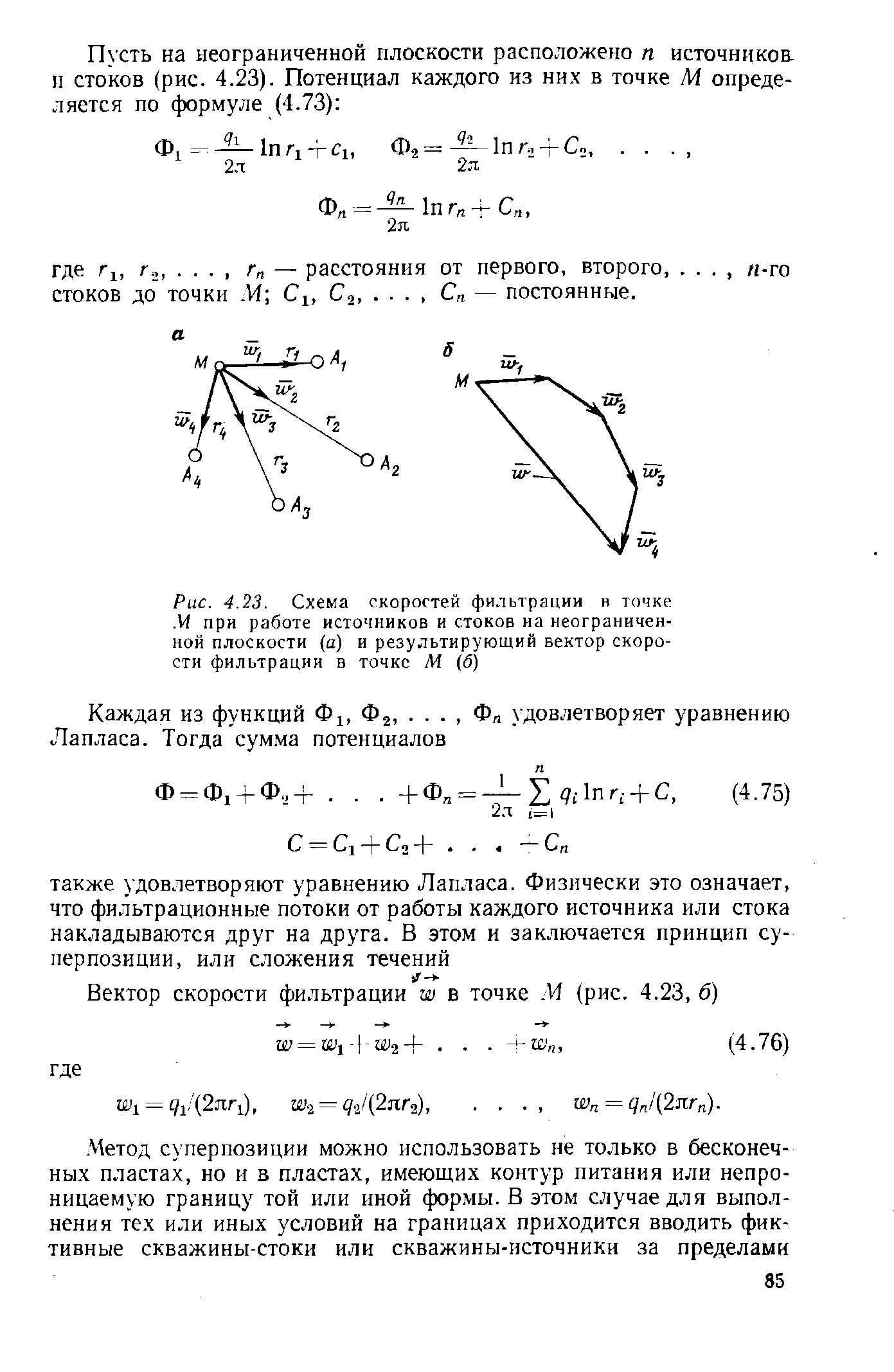
Пусть на неограниченной плоскости расположено и источников и стоков (рис. 1, а). Потенциал каждого из них в точке М определяется по формуле (2.4):

, , ….,

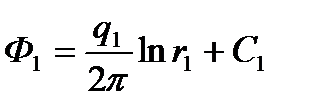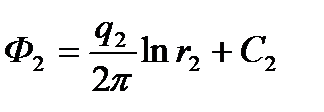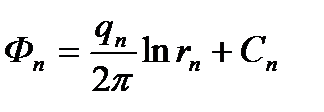
где r₁, r₂,... r_n - расстояния от первого, второго, ... n-то стоков до точки М; С₁, С₂,..., C_n - постоянные.

Каждая из функций Ф₁, Ф₂,..., Ф_n удовлетворяет уравнению Лапласа.