Приток жидкости к скважине в пласте с прямолинейным контуром питания
Пусть в полубесконечном пласте с прямолинейным контуром питания, на котором потенциал равен Фк, работает одна добывающая скважина А с забойным потенциалом Фс (рис. 4). Необходимо найти дебит скважины q, потенциал и скорость фильтрации в любой точке пласта.
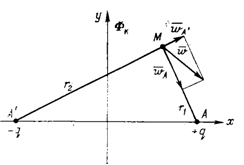
Если бы пласт был неограниченным или контур питания был бы кругом, в центре которого расположена скважина. При этом условие постоянства потенциала на прямолинейном контуре питания не выполняется, так как расстояние г разных точек контура питания от скважины А неодинаково.
Для решения задачи используем метод отображения источников и стоков. Зеркально отобразим скважину-сток А относительно контура питания и дебиту скважины-изображения А' припишем противоположный знак, т. е. будем считать ее скважиной источником. Теперь рассмотрим в бесконечном пласте совместную работу двух скважин: скважины-стока А с дебитом +q и скважины-источники А' с дебитом -q. Потенциал в любой точке М, находящейся на расстоянии r1 от скважины A и на расстоянии r2 от скважины А':
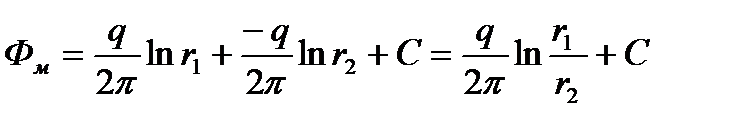 (1.4)
(1.4)
Потенциал на контуре питания можно выразить, подставив в (1.4) r1 = r2. В результате получим
Ф = С = Фк, (1.5)
т. е. потенциал на контуре питания действительно постоянен. Тогда из (1.4) с учетом (1.5) потенциал на забое скважины А (r1 = rc, r2 = 2а) можно выразить так:
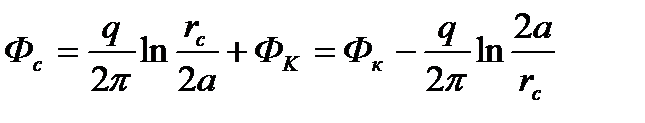 (1.6)
(1.6)
Из (1.6) выражение для дебита скважины А, приходящегося на единицу толщины пласта, получим в следующем виде:
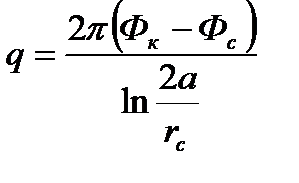 (1.7)
(1.7)
Если бы контур питания был окружностью радиуса а, то дебит скважины был бы равен (по формуле Дюпюи):
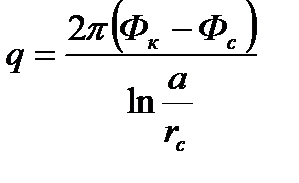
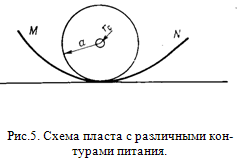
В реальных условиях форма контура питания MN (рис. 5) часто бывает неизвестна, но она заключена между окружностью и прямой линией.
Следовательно, дебит скважины в этих условиях будет находиться в пределах
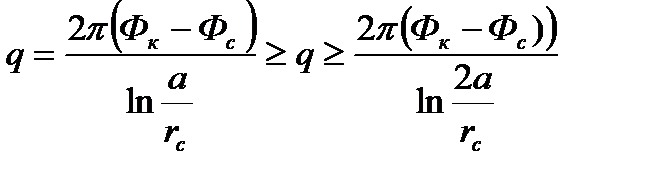
Для определения потенциала в любой точке М (см. рис. 5) воспользуемся формулой (1.4) с учетом (1.5):
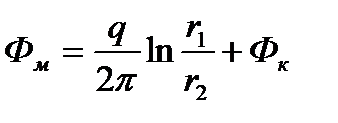 (1.8)
(1.8)
Скорость фильтрации равна геометрической сумме скоростей фильтрации, вызванных работой реальной скважины-стока А и фиктивной скважины-источника А' (см. рис. 5), т. е.
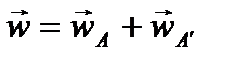
где 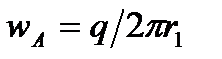 и направлена к скважине A;
и направлена к скважине A; 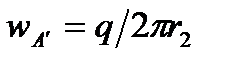 и направлена от скважины А'.
и направлена от скважины А'.
На контуре питания, где r1 = r2, скорость фильтрации перпендикулярна контуру питания.
Из формулы (23) следует, что уравнение эквипотенциалей имеет вид:
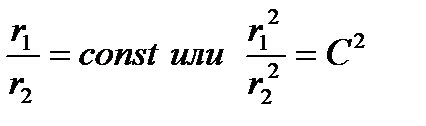 (1.9)
(1.9)
Если выразить 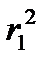 и
и 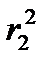 через координаты точки М (х, у) и координаты центров скважин А (а, 0) и А' (-а, 0), то будем иметь
через координаты точки М (х, у) и координаты центров скважин А (а, 0) и А' (-а, 0), то будем иметь 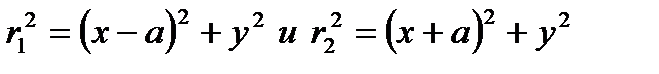 . Следовательно, уравнение (1.9) представляет собой уравнение окружности с центром на оси х. Меняя значение константы С2, получим семейство эквипотенциалей - окружностей с разными радиусами и с центрами, расположенными в разных точках оси х. Контур питания является эквипотенциалью, т. е. окружностью с бесконечно большим радиусом.
. Следовательно, уравнение (1.9) представляет собой уравнение окружности с центром на оси х. Меняя значение константы С2, получим семейство эквипотенциалей - окружностей с разными радиусами и с центрами, расположенными в разных точках оси х. Контур питания является эквипотенциалью, т. е. окружностью с бесконечно большим радиусом.
Семейство линий тока будет представлять собой окружности, проходящие через центры обеих скважин, которые лежат на прямолинейном контуре питания (рис. 6).
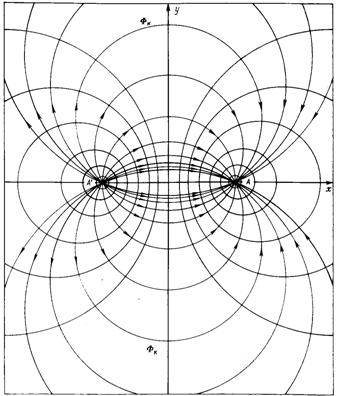
Рис. 6. Семейства линий тока и изобар в потоке жидкости к скважине в пласте с прямолинейным контуром питания.
При этом эквипотенциали (изобары) всегда ортогональны линиям тока. На рис. 6 показаны семейства линий тока и изобар при притоке жидкости к скважине в пласте с прямолинейным контуром питания.
4. Приток жидкости к скважине, расположенной вблизи непроницаемой прямолинейной границы
Такая задача может возникнуть при расположении добывающей скважины возле сброса или около границы выклинивания продуктивного пласта. В этом случае реальную скважину-сток зеркально отображают относительно непроницаемой границы, и дебиту скважины-изображения приписывают тот же знак, что и дебиту реальной скважины. Рассматривая приток жидкости к двум равнодебитным скважинам, нетрудно установить, что скорость фильтрации на непроницаемой границе будет направлена вдоль границы, т. е. граница является линией тока и фильтрация через нее отсутствует. Дебит скважины в этом случае определяется из уравнений (9) и (10) для n = 2 в пласте с удаленным контуром питания:
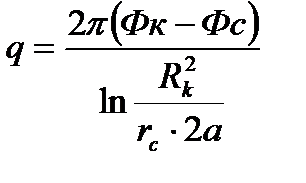
где, 2а - расстояние между реальной и воображаемой скважинами.
Дата добавления: 2015-02-10; просмотров: 2213;
