Приток жидкости к группе скважин в пласте с удаленным контуром питания

Пусть в горизонтальном пласте толщиной h, расположена группа скважин А₁, А₂, . . . , А_n радиусами r_сi ,работающих с различными забойными потенциалами Ф_{сi ,}где (i=1, 2, ... , n (рис. 3).

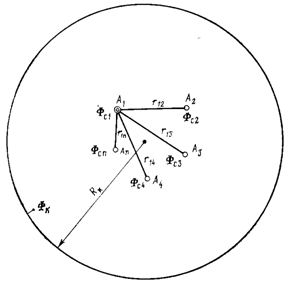
Расстояния между центрами i-й и j-и скважин известны (r_ij =r_ji). Так как контур питания находится далеко от всех скважин, то можно приближенно считать, что расстояние от всех скважин до всех точек контура питания одно и то же и равно R_k. Потенциал Ф_к на контуре питания считается заданным. Требуется определить дебит каждой скважины и скорость фильтрации в любой точке пласта. Поместив мысленно точку М последовательно на забой каждой скважины, получим выражения для забойного потенциала на них

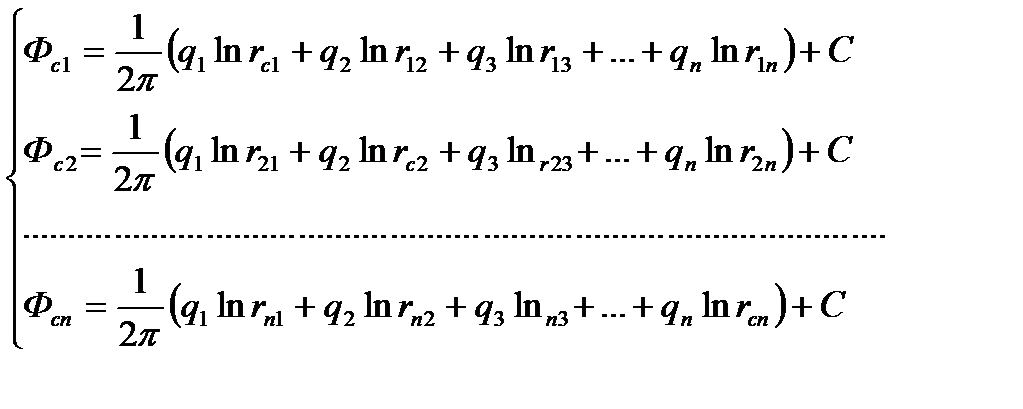(1.1)

Здесь приближенно принято, что расстояние от точки на стенке данной скважины i до центра любой другой скважины j равно расстоянию между центрами этих скважин, так как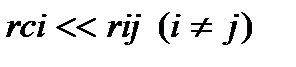

Система (1.1) состоит из n уравнений и содержит n + 1 неизвестных (n дебитов скважин и постоянную интегрирования С). Дополнительное уравнение получим, поместив точку М на контур питания:

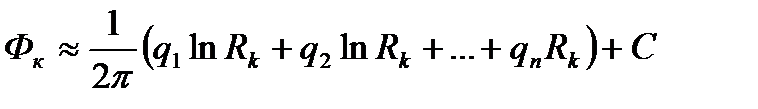(1.2)

Вычитая почленно каждое из уравнений (1.1) и (1.2), исключим постоянную С и получим систему из n уравнений, решив которую, можно определить дебиты скважин q₁, q₂, . . . , q_n, если заданы забойные Ф_С1, Ф_С2 , … , Ф_сn и контурный Ф_к потенциалы. Точно так же можно решить и обратную задачу определения потенциалов по известным дебитам q_i ( i= 1, 2, . . . , n).

Имеем:

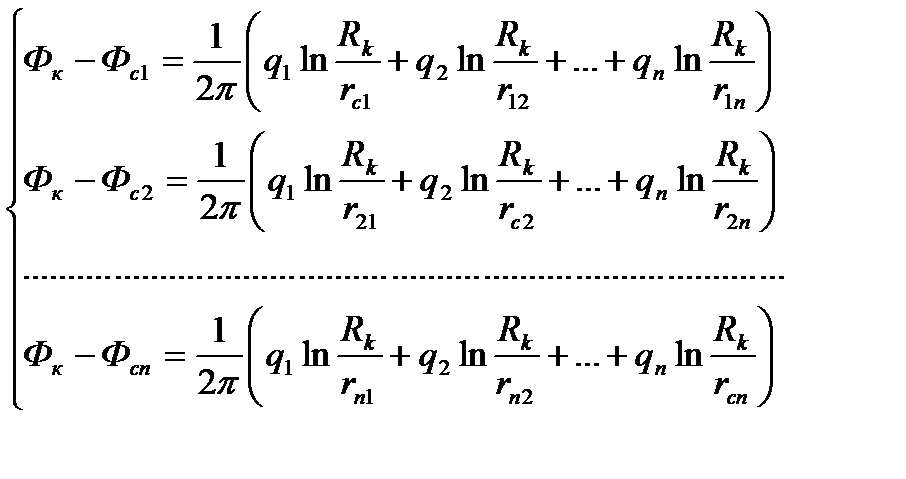(1.3)

Скорость фильтрации w в любой точке пласта М определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины:

,

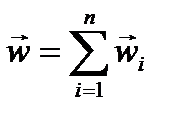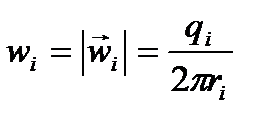
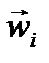направлена по радиусу от точки М к данной скважине-стоку. Если на месторождении находятся в эксплуатации десятки, а то и сотни скважин, то, очевидно, надо составить десятки или сотни таких уравнений, как (1.1). Решение такой сложной системы уравнений возможно с помощью ЭВМ.