Приток жидкости к скважине, эксцентрично расположенной в круговом пласте

Пусть в плоском пласте постоянной толщиной h с круговым контуром питания радиуса R_к, на котором поддерживается постоянный потенциал Ф_к, на расстоянии 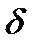от центра круга расположена скважина-сток А, на которой поддерживается постоянный потенциал Ф_с (рис. 7). Требуется определить дебит скважины и потенциал в любой точке пласта.

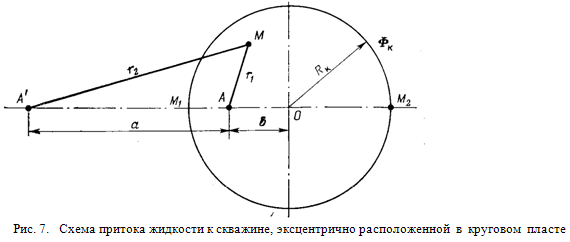
Отобразим скважину-сток А фиктивной скважиной-источником А', расположенной от скважины А на расстоянии а и лежащей на продолжении OА. Это расстояние а определим из условия постоянства потенциала на окружности радиуса R_к, для чего выразим потенциал в двух точках М₁ и М₂ контура питания, взятых на пересечении прямой АА' с контуром питания.

По методу суперпозиции потенциалы в этих точках будут иметь следующие выражения:

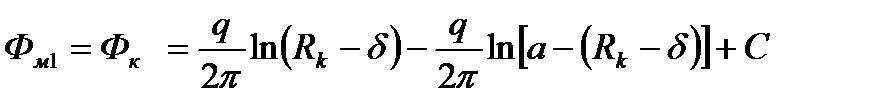(1.10)

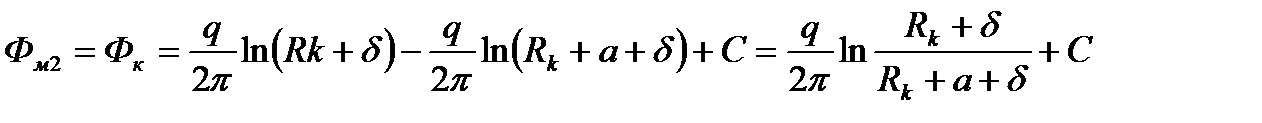1.11)

Из равенства правых частей формул (1.10) и (1.11) найдем расстояние между скважинами А и А':

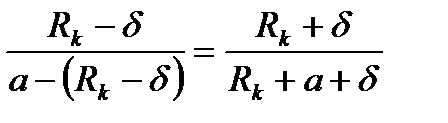
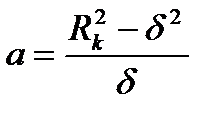(1.12)

Для того чтобы определить дебит скважины А, запишем выражение потенциала на ее забое:

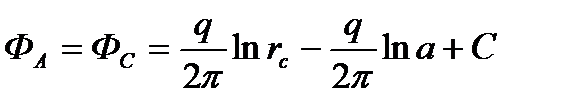(1.13)

Вычитая (1.13) из (1.10), получим:

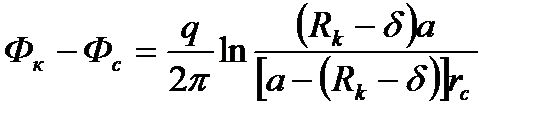(1.14)

Подставляя теперь выражение (1.12) в (1.14), находим:

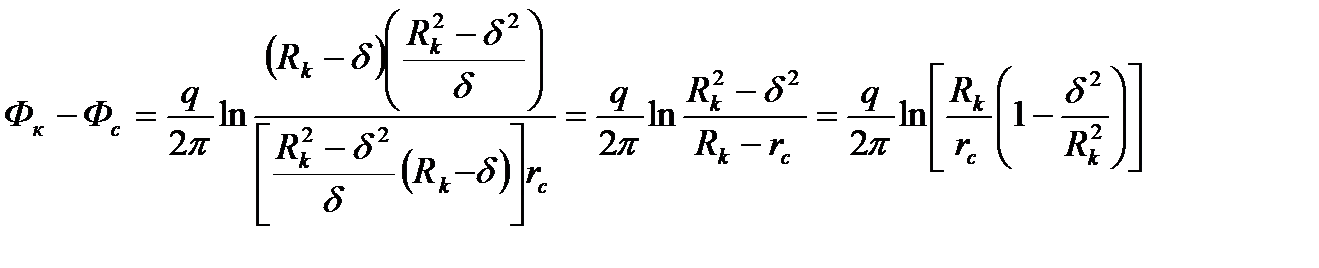(1.15)

Из формулы (1.15) получаем дебит скважины А, эксцентрично расположенной в круговом пласте:

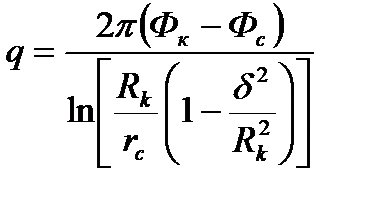(1.16)

При эксцентриситете 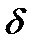= 0 формула (1.16) обращается в формулу Дюпюи.

Потенциал в любой точке пласта М, находящейся на расстоянии r₁ от скважины A и на расстоянии r₂ от скважины А', можно выразить так:

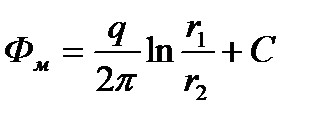(1.17)

Вычитая из (1.17) выражение (1.13) и учитывая (1.12), получим:

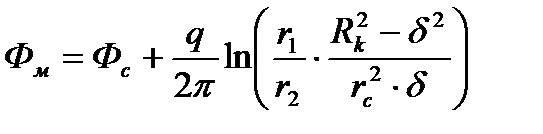(1.18)

Выражение для потенциала в точке М можно получить также и вычитанием из уравнения (1.10) или (1.11) уравнения (1.17):

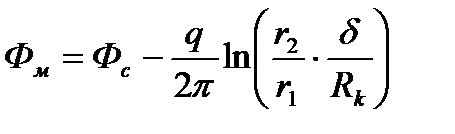(1.19)

6. Приток жидкости к бесконечным цепочкам и кольцевым батареям скважин

На примере притока жидкости к нескольким рядам или кольцевым батареям скважин ознакомимся с широко применяемым при проектировании разработки нефтяных месторождений методом эквивалентных фильтрационных сопротивлений, предложенным Ю. П. Борисовым и основанным на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Рассмотрим без вывода задачу о притоке жидкости к одной цепочке скважин, расположенных на расстояниях 2 друг от друга и на расстоянии L от прямолинейного контура питания. Пусть на контуре питания задан постоянный потенциал Ф_к, на забоях скважин - потенциал Ф_с (рис. 8). Требуется определить дебит каждой скважины и суммарный дебит n скважин в цепочке.

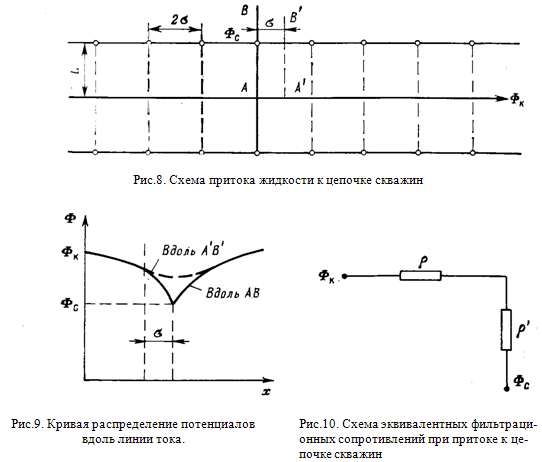
Решение задачи заключается в следующем. Цепочка скважин-стоков отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте.

Вдоль прямой АВ, проходящей через скважины (как говорят, вдоль главной линии тока), частицы жидкости будут двигаться наиболее быстро. Прямую А’В’ и ей подобные, делящие расстояние между скважинами пополам, в силу симметрии потока можно рассматривать как непроницаемые границы, вдоль которых движение будет наиболее медленным. Они называются нейтральными линиями тока. Характер распределения потенциалов вдоль этих прямых АВ и А'В' показан на рис. 9. Задача решается методом суперпозиции. Результаты решения показывают, что на расстоянии от контура питания до половины расстояния между скважинами движение жидкости практически прямолинейное и падение потенциала на этом участке происходит по закону прямолинейной фильтрации. Основное падение потенциала происходит вблизи скважины, где характер движения близок к радиальному. При этом дебит каждой скважины цепочки выражается следующей формулой:

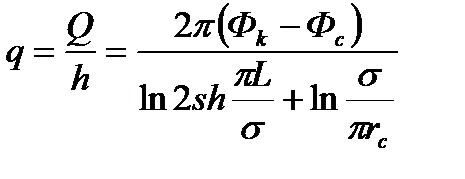
где 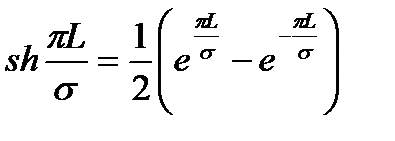— гиперболический синус.

В случае, когда 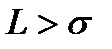, величина 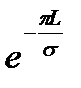очень мала и тогда:

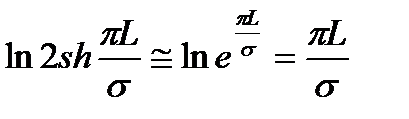
Отсюда следует, что при 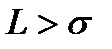дебит скважины:

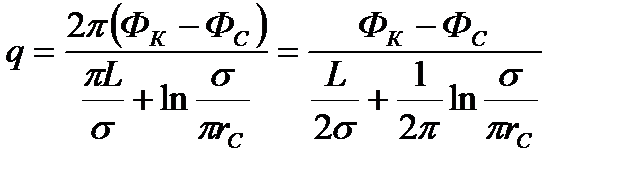(1.20)

Вводя обозначения:

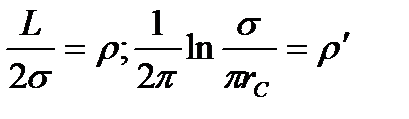
формулу (1.20) представим в виде:

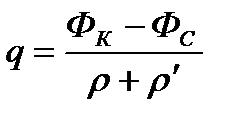(1.21)

аналогичному закону Ома.

Величина 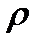, по терминологии Ю. П. Борисова, называется внешним фильтрационным сопротивлением батареи, 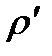- внутренним. Таким образом, приток жидкости к цепочке скважин можно представить схемой эквивалентных фильтрационных сопротивлений, показанной на рис. 10.

Аналогом объемного расхода q служит сила тока, а аналогом разности фильтрационных потенциалов - разность электрических потенциалов. Суммарный дебит всей прямолинейной цепочки из n скважин:

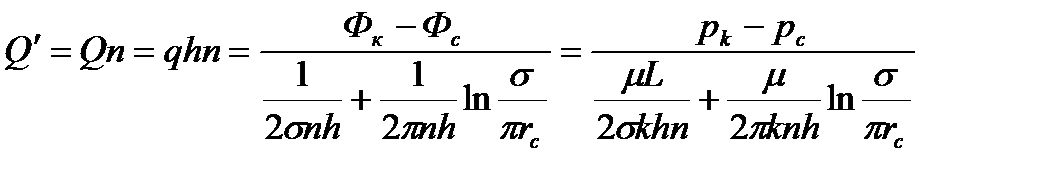(1.22)

Из формулы (1.22) получили выражение для внешнего фильтрационного сопротивления цепочки:

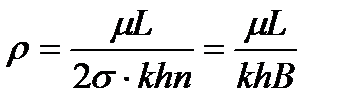
которое представляет собой сопротивление потоку жидкости от контура питания до галереи длиной 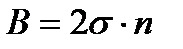, расположенной на расстоянии L, от контура питания, а внутреннее сопротивление:

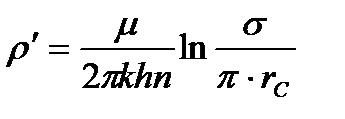
выражает сопротивление, возникающее при подходе жидкости к скважинам в зоне радиусом 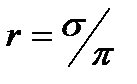, где фильтрация практически плоскорадиальная.

Пусть теперь полубесконечный пласт с прямолинейным контуром питания разрабатывается тремя параллельными цепочками скважин с числом скважин в каждой n₁, n₂, n₃. Пусть скважины в каждой цепочке имеют одинаковые радиусы r_c1, r_c2, r_c3 и забойные давления p_c1, р_c2, р_с3, суммарные дебиты цепочек составляют , , .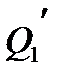

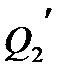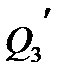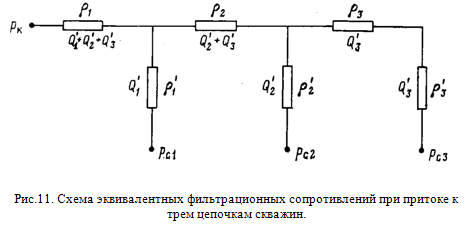
Схема соответствующих эквивалентных фильтрационных сопротивлений будет теперь разветвленной (рис.11).

Расчет схемы проводится аналогично расчету электрических разветвленных цепей по законам Ома и Кирхгофа. Составляются алгебраические линейные уравнения по числу неизвестных (либо дебитов 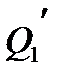, , 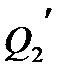, 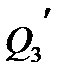либо забойных давлений p_c1, р_c2, р_с3 ). При этом очевидно, внешние сопротивления будут равны:

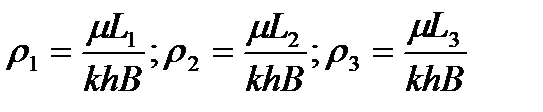
где L₁,L₂, L₃ - расстояния соответственно от контура питания до первой цепочки, между первой и второй цепочками, между второй и третьей цепочками.

Внутренние сопротивления определяются по формулам:

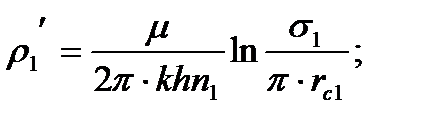
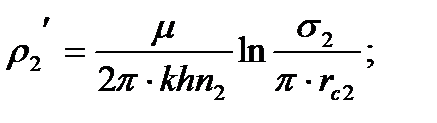
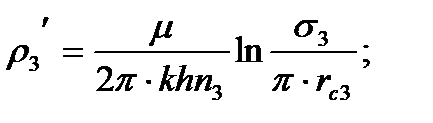(1.23)

Отметим, что приток жидкости к трем кольцевым батареям скважин, соосным круговому контуру питания, рассчитывается по той же схеме эквивалентных фильтрационных сопротивлений (см. рис. 11), что и для цепочек скважин. При этом внешние фильтрационные сопротивления будут выражаться так:

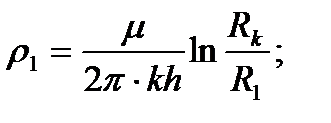
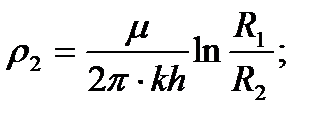
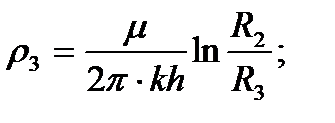
где R₁, R₂, R₃ - радиусы батарей.

Внутренние фильтрационные сопротивления определяются по формулам (1.23).