Нелинейные системы автоматического управления

Рассмотрим САУ с одним входом и одним выходом, будем считать 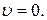Пусть модель объекта имеет вид

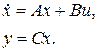(9.19)

При этом методе синтеза [6] закон управления выражается формулой

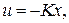(9.20)

где 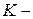вектор коэффициентов

Структура замкнутой САУ приведена на рис. 9.10.

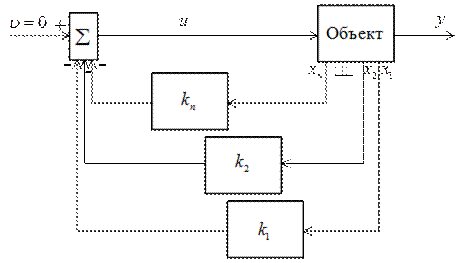
Рис. 9.10

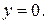Так как то назначение САУ поддерживать значение Такую САУ называют регулятором состояния.

Рассмотрим пример спутника (рис. 9.11) с передаточной функцией [6].

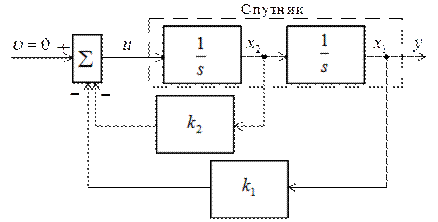
Рис. 9.11

Модель объекта (спутника) будет иметь вид

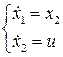или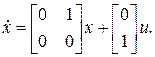

Для замкнутой САУ, где , имеем

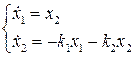или 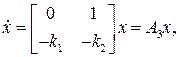(9.21)

где 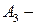матрица коэффициентов замкнутой САУ.

Характеристическое уравнение замкнутой САУ имеет вид

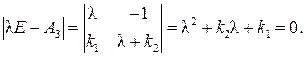(9.22)

Пусть корни его будут 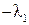и 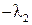, тогда характеристическое уравнение желаемой замкнутой системы имеет вид

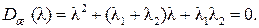(9.23)

Синтез системы заключается в выборе 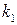и 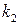в (9.22), которые бы соответствовали коэффициентам уравнения (9.23), т.е.

(9.24)

Рассмотрим общий принцип синтеза САУ.

Пусть

.

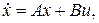
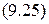
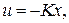
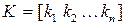Подставляя (9.26) в (9.25), получим

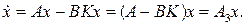(9.27)

Характеристическое уравнение замкнутой САУ имеет вид

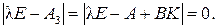(9.28)

Если корни 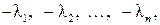то желаемое характеристическое уравнение замкнутой САУ будет иметь вид

(9.29)

Приравнивая (9.28) и (9.29), имеем

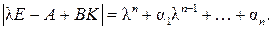(9.30)

В этом уравнении 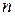неизвестных 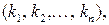но они могут быть найдены путем приравнивания коэффициентов при 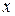в одинаковых степенях.

Пусть передаточная функция объекта будет иметь вид

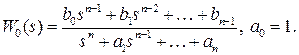(9.31)

Уравнения состояния при 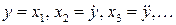имеют вид

(9.32)

Матрица 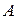является фробениусовой, а уравнение объекта соответствует нормальной форме.

При законе модального уравнения для замкнутой САУ в
матрице 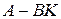член 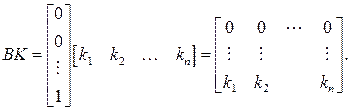Матрица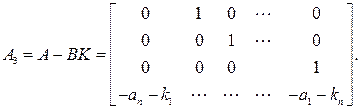

Характеристическое уравнение замкнутой САУ имеет вид

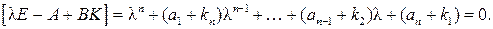
Желаемое характеристическое уравнение замкнутой САУ будет

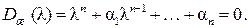
Из двух последних уравнений следует:

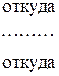
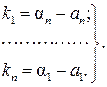(9.33)

Последняя система представляет собой общее решение задачи синтеза путём размещения полюсов для САУ с одним входом и одним выходом, но для этого исходная модель САУ должна быть в нормальной форме (матрица 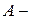фробениусова).

Аккерман предложил формулу, которая позволяет перейти от произвольной формы уравнений состояния к нормальной, затем найти 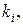а потом перейти к исходной структуре.

Формула Аккермана имеет вид

(9.34)

где 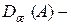матричный полином, образованный путём использования коэффициентов желаемого характеристического уравнения

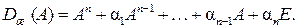(9.35)

Последние выражения (при 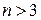) рассчитываются на компьютере.

Пример 9.3. Для спутника 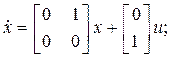характеристическое уравнение

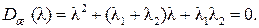
Используем формулу Аккермана. Определи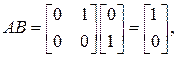м затем 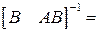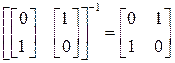. Образуем матричный полином

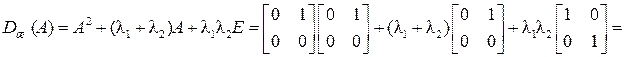
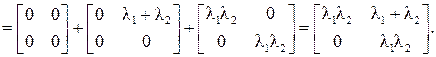
По формуле Аккермана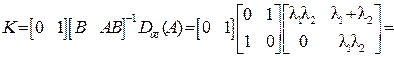
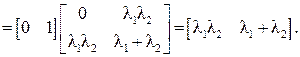Как видим, результаты совпали с (9.24).

Остановимся на вопросе формирования полюсов передаточной функции замкнутой САУ, исходя из заданных показателей качества на основе корневых оценок.

Определим границу расположения желаемых полюсов (корней) САУ. Исходя из заданного времени переходного процесса 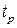, в силу (7.4) находим 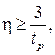если ближайший к мнимой оси корень вещественный и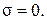

Угол сектора комплексных корней связан с перерегулированием в силу (7.6) соотношением 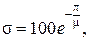где 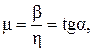если ближайшая к мнимой
оси – пара комплексных сопряжённых корней и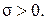

Из соотношения 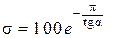следует

(9.36)

Пример 9.4.Рассмотрим оба случая для САУ из предыдущего примера.

1. Если 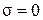(ближайший корень – вещественный) и 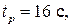то .

Возьмём оба корня вещественных: 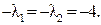Тогда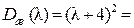

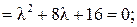
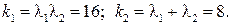
2. Пусть 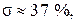а 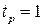с, т.е. Тогда .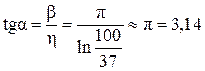

При 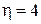значение ; ,

.

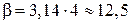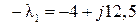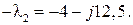
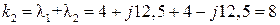Примечание. При определении полюсов не следует чрезмерно увеличивать 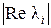, так как при этом увеличиваются значения 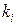, а для повышения реакции инерционных объектов надо на их вход подавать большие сигналы, что может привести к насыщению элементов и сделать САУ нелинейной [6].

Нелинейные системы автоматического управления