Химическая кинетика и катализ. Ферменты – катализаторы (ускорители) всех биохимических реакций, в реакциях они не расходуются

Ферменты – катализаторы (ускорители) всех биохимических реакций, в реакциях они не расходуются.

Скорости химических реакций зависят от температуры. Формула Аррениуса для константы скорости реакции.

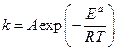
где 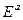- энергия активации, характеризующая барьер, который частица должна преодолеть для осуществления реакции.

Эта формула следует из распределения Больцмана по энергиям; экспонента указывает на долю молекул, обладающих достаточной для реакции энергией активации 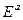при данной температуре T. k – определяет скорость реакции.

В обратимой реакции скорости равны 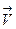и .

,

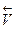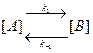где [A] и [B] – концентрации веществ А и В.

.

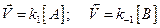В равновесии 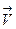= 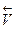, и константа равновесия K = /

.

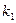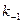
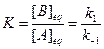Разность свободных энергий продуктов реакции и исходных реагентов равна:

;

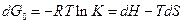где dH и dS – разность энтальпий и энтропий. Реакция возможна, если

dG < 0 (свободная энергия понижается).

Это необходимое условие, но не достаточное для реакции. 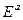может быть большой, при этом константа скорости мала, и реакция не идет.

Катализатор служит для понижения активационного барьера, т.е. уменьшения разности между энергией фермент-субстратного комплекса и энергией активации реагентов.

Эйринг предложил теорию абсолютных скоростей реакции (теория переходных состояний или активированного комплекса). При этом в теории вводятся следующие допущения:

1. Предполагается, что ход реакции не нарушает больцмановского распределения молекул по состояниям с разной энергией.

2. Прохождение реакции требует преодоления энергетического барьера.

dG =G1-G2 , dG- разность свободных энергий начального и конечного состояний.

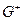- свободная энергия активации в процессе 1 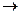2

Находят число систем, находящихся в некотором интервале δ реакционной координаты ξ на вершине барьера. Среднее время прохождения через барьер: 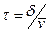, где 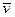- средняя скорость перемещения частиц на вершине барьера.

Скорость реакции — это число систем, преодолевающих энергетический барьер в единицу времени. Средняя скорость движения системы равна:

.

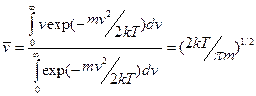В уравнении (5) воспользовались распределением Максвелла-Больцмана по кинетическим энергиям 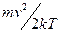. Скорость реакции, т.е. число переходов через барьер в единицу времени:

,

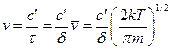где 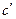- число систем в единице объема, находящихся в пределах отрезка δ.

Вместе с тем

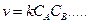
где 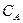, 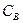- концентрации реагентов

Из (6) и (7) имеем

.

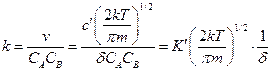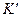— константа равновесия для перехода реагентов A,B…. в активированное состояние.

Константа равновесия выражается через статсуммы z:

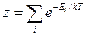
где 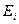- энергия i-го состояния системы. Суммирование ведётся по всем состояниям. В нашем случае:

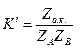
где 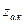, 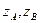— статсуммы для активированного комплекса и реагентов.

Для поступательного движения частицы набор состояний непрерывен, сумма (9) заменяется интегралом, который равен

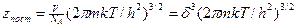
где h – постоянная Планка, m- масса частицы, 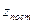- это статсумма по трем степеням свободы поступательного движения.

Т.к. система имеет только одну такую степень свободы — вдоль направления реакции, получаем

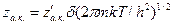
где 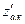- статсумма для активированного комплекса по всем степеням свободы, кроме поступательной.

Из (8), (10), (12) получаем:

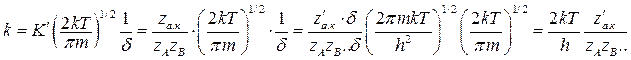
Условная длина сократилась

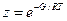
и, следовательно,

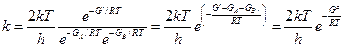
Здесь 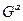— избыток свободной энергии активированного комплекса по сравнению с суммарной свободной энергией реагентов, т.е. свободная энергия активации. При выводе (15) полагалось, что, достигнув активационного барьера, система обязательно вступит в реакцию. Этого может и не быть. Поэтому вводят трансмиссионный коэффициент χ ≤ 1

Тогда формула Эйринга для константы скорости гомогенной газовой реакции:

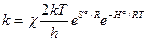
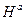, — энтропия и энтальпия активации. Условие χ = 1 отвечает адиабатическому течению реакции (т. е. когда параметры изменяются медленно); χ << 1 — для неадиабатического процесса (может достигать ~ 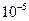). В газовых реакциях χ обычно стремится к 1 (т.е. реакции эти обычно адиабатичны; kT/h при обычных T ~ ).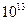

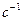Сравнивая (1) и (16) видим, (отождествляя энтальпию и энергию активации) что в формуле Аррениуса

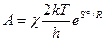
Значения параметров активации определяют по температурной зависимости k. При χ = 1

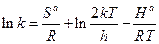
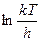слабо зависит от T, и этим членом можно пренебречь. По наклону прямой lnk от 1/T находят 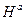, а по отрезку, отсекаемому на оси ординат, — .

Нелинейность зависимости lnk от 1/T свидетельствует об усложнении процесса (о его кооперативности, в таком процессе 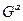зависит от числа уже прореагировавших систем и тем самым от 1/T, т.е. не постоянна). Нельзя трактовать h/(kT) как время существования активированного комплекса, т.к. за 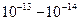с не может установиться статистическое равновесие. В реальности время существования системы в состоянии, отвечающем значениям реакционной координаты от ξ до ξ + δ, пропорционально δ. Это время аналогично времени существования состояний в теории Максвелла-Больцмана. Из малости h/(kT) нельзя делать вывод о невозможности установления равновесия между активированным комплексом и реагентами. Термин "активированный комплекс" относится к атомной системе, претерпевающей превращения, и не означает состояние метастабильного комплекса.

Теория Эйринга применима к реакциям в газах, но не в жидкой фазе. Общий метод качественного рассмотрения пригоден для различных кинетических процессов (диффузия, вязкое течение и т.д.).

В ряде случаев реакция идет без преодоления активационного барьера, посредством туннельного эффекта (квантовомеханического просачивания через барьер в реакциях переноса 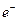или протона). В этом случае скорость реакции практически не зависит от T).