Графическая обработка результатов измерений
Очень часто обработку результатов производят графическим способом, который сразу даёт наглядное представление о характере зависимости одной величины от другой. Также по графикам определяют характерные параметры функциональной зависимости.
Известно, что функциональную зависимость у(х) можно представить тремя способами: уравнением; таблицей; графиком.
Напомним некоторые виды зависимостей между двумя переменными, которые традиционно обозначим буквами х и у (х – независимая переменная – аргумент);(у – переменная, зависящая от х – функция; y = f(x)).
Графики соответствующих функций представлены на (рис. 1–4). Также на этих рисунках показаны процедуры определения угловых коэффициентов линейных зависимостей и определения производных нелинейных зависимостей методом графического дифференцирования.
Уравнение: у = сх;
с = const – угловой коэффициент.

| Уравнение: 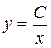 ; ;
 С = const (постоянная величина) С = const (постоянная величина)
| |||
Уравнение: у = b + сх;
| Уравнение: у = у0есх; с < 0.
 е = 2,718…….. е = 2,718……..
|
При измерениях зависимость между двумя физическими величинами получается в виде таблицы, по которой и производится построение графика. Чтобы работать с данными измерений было удобно, при оформлении таблиц следует придерживаться некоторых простых правил.
Таблицы для записи данных к каждой лабораторной работе готовят заранее по описанию лабораторной работы, во время домашней подготовки к получению допуска. Лист с таблицами должен быть озаглавлен: номер и название лабораторной работы, Ф.И.О. студента, номер группы, дата проведения измерений.
В заголовке таблицы указывают обозначение измеряемой величины и, через запятую, её единицу измерения. Данные прямых измерений записывают в единицах шкалы прибора (в миллиметрах (мм), в секундах (с), в граммах (г) и др.), а результаты расчётов – в единицах СИ.
Записи в таблицах нужно делать аккуратно и разборчиво, и не карандашом, а перьевой или шариковой ручкой! В столбцах численные значения каждой измеренной или рассчитанной величины записываются одно под другим так, чтобы одинаковые разряды и запятые располагались на одной вертикали. Не следует исправлять цифры! Лучше зачеркнуть неверное значение и написать правильное рядом или выше.
При записи малых и больших чисел нужно использовать множитель, указывающий порядок числа: не 0,00147 м, а 1,47×10–3 м, или 1,47 мм; не 30400 с2, а 3,04×104 с2.
График наглядно представляет зависимость у(х)между двумя переменными. Независимая переменная х откладывается по горизонтальной оси, зависимая у – по вертикальной оси. Выполняется график на миллиметровой бумаге.
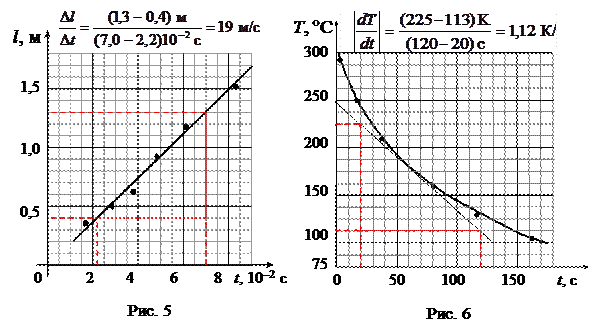
Сначала вычерчиваются координатные оси, на которые наносится масштаб. В конце оси указывается буквенное обозначение откладываемой величины, её единица измерения, а также порядок масштаба (рис. 5).
Порядок масштаба определяется числом нулей, стоящих либо перед значащими цифрами, либо после них. Масштаб содержит лишь значащие цифры. Если, например, сопротивление проводника в опыте менялось от 0,0021 до 0,0086 Ом, в конце оси ставится множитель 10–3 Ом, а деления масштаба изменяются соответственно от 2,0 до 9,0.
Напоминаем: масштаб – это набор чисел на оси, отделённых друг от друга одним и тем же интервалом. Интервалы следует выбирать кратными числам 1, 5, 2 или 4, с множителем 10п. Применять интервал 3 не рекомендуется, потому что неудобно определять положение экспериментальных точек.
Деления на осях графикавыбирают независимо,и значения наносят равномерновдоль всей оси.Не следует, однако, писать численные значения слишком часто, достаточно 3–5 делений с числами. Недопустимонаносить на координатные оси значения, стоящие в таблице.
Точка пересечения осей графика должна быть близка к минимальным значениям из таблицы: первое деление масштаба на каждой оси выбирается близким к наименьшему значению откладываемой величины (т.е. может начинаться не с нуля), если наличие начала координат необязательно. Конечное значение масштаба определяется наибольшим значением откладываемой величины (рис. 6).
Следует выполнять ещё одно правило: график должен быть близок к квадрату, т. е. длины обеих осей должны быть примерно одинаковыми. Этого добиваются соответствующим подбором масштабов (см. рис. 5 и 6). Кроме того, выбранный Вами масштаб должен позволить нанести все точки из таблицы наблюдений с имеющейся там точностью: все значащие цифры из таблицы наблюдений должны легко определяться на соответствующих осях. Поскольку на мелких графиках последнее требование вряд ли выполнимо, то рекомендуемый размер – это квадрат со сторонами по 12…16 см, чтобы лист, на котором выполнен график, не «вылезал» за пределы тетрадного листа.
В табл. 5–6 представлены данные, по которым построены графики на рис. 5, 6.
| Таблица 5 | Таблица 6 | |||||
| № п/п | l,м | t, c | № п/п | Т,К | t, c | |
| 0,35 | 0,017 | 3,5 | ||||
| 0,50 | 0,027 | 18,0 | ||||
| 0,62 | 0,038 | 38,2 | ||||
| 0,92 | 0,048 | 80,6 | ||||
| 1,18 | 0,062 | 117,2 | ||||
| 1,51 | 0,083 | 162,1 |
После того как нанесены все точки, следует провести по ним плавную (сглаженную) кривую (или прямую) так, чтобы сумма отклонений экспериментальных точек от графика была минимальной. При проведении прямых графиков удобно пользоваться прозрачной линейкой.
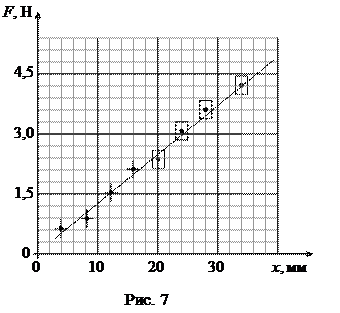 Добавим, что на графиках часто указывают также погрешности, с которыми определены значения, по которым строится график. Для этого вместо каждой точки на координатной плоскости наносится прямоугольник, или крест, длина сторон которых равна абсолютной погрешности числа в таблице. Пример применения такого, более информативного метода, приведён на рис. 7. По оси абсцисс откладываются значения удлинения пружины (Dх), определённые с погрешностью 1 мм, по оси ординат – величина силы упругости F, измеренная с абсолютной погрешностью 0,3 Н. Для примера абсолютные погрешности показаны на графике как первым способом (крест), так и вторым (прямоугольник).
Добавим, что на графиках часто указывают также погрешности, с которыми определены значения, по которым строится график. Для этого вместо каждой точки на координатной плоскости наносится прямоугольник, или крест, длина сторон которых равна абсолютной погрешности числа в таблице. Пример применения такого, более информативного метода, приведён на рис. 7. По оси абсцисс откладываются значения удлинения пружины (Dх), определённые с погрешностью 1 мм, по оси ординат – величина силы упругости F, измеренная с абсолютной погрешностью 0,3 Н. Для примера абсолютные погрешности показаны на графике как первым способом (крест), так и вторым (прямоугольник).
Дата добавления: 2015-02-07; просмотров: 4836;


