Погрешности измерений. Внимание! Данные измерений, т.е
Внимание! Данные измерений, т.е. показания приборов – не округляются!
1. Любые измерения имеют погрешности. Абсолютно точных измерений не бывает! Погрешности определяют по-разному в зависимости от вида измерения.
2. Виды измерений:
· прямые – результат считывают по шкале прибора (линейки, секундомера, вольтметра, пирометра и др.);
· косвенные – результат определяется расчётом (объём параллелепипеда по длине сторон; мощность по силе тока и напряжению; скорость по пути и времени; плотность по массе и объёму и др.);
· однократные;
· многократные.
3. Виды погрешностей:
· приборные – погрешность равна цене деления прибора;
· случайные – при многократных измерениях одной и той же величины точным прибором;
· систематические – измерения неисправным прибором (секундомер спешит или отстаёт, сдвинут нуль шкалы и др.).
4. Результат измерений величины Х представляют в виде:
| X = Xи ± DХ, | (1) |
где Xи – показания прибора (при прямых измерениях), или результат расчёта (при косвенных измерениях), или среднее значение (при многократных измерениях); DХ – абсолютная погрешность измерения.
Такая запись означает, что истинное значение измеренной величины лежит в интервале от (Xи – DХ) до (Xи + DХ).
5. Случайные погрешностиопределяют методами математической статистики, в которой предполагается, что наиболее близким к истинному значению измеряемой величины Х является среднее арифметическое áХñ от результатов измерений этой величины. Среднее арифметическое вычисляется по общим правилам – сумма всех измеренных значений делится на количество измерений:
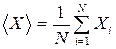 , ,
| (2) |
где N – число измерений; i – номер измерения; Хi – значение, полученное при измерении с номером i.
6. Абсолютная погрешность DХi конкретного (i-го) измерения определяется как разность между средним и конкретным значениями:
| DХi = áХñ – Хi , | (3) |
то есть является отклонением от среднего значения. Как видно из определения, DХi может быть и положительной, и отрицательной величиной.
7. Средняя абсолютная погрешность áDХñ определяется как среднее арифметическое отклонений (3), взятых по модулю (т. е. без учёта знака!):
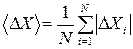 . .
| (4) |
При записи результата измерений áDХñ округляется до одной значащей цифры (или до двух цифр, если первая значащая цифра – единица).
8. Результат измерений со случайными погрешностями представляют в виде
| X = áХñ ± áDХñ. | (5) |
Такая запись означает, что истинное значение измеренной величины лежит в интервале от (áХñ – áDХñ) до (áХñ + áDХñ). При записи результата измерений среднее значение áХñ округляют так, чтобы последняя значащая цифра в этом числе имела тот же разряд, что и áDХñ.
Например, при расчётах среднее значение величины Х получилось равным 2,326, а средняя абсолютная погрешность при расчётах с тремя значащими цифрами оказалась равной 0,0377. Тогда, в соответствии с правилами, результат следует записать в следующем виде:
X = 2,33 ± 0,04.
Если при том же áХñ средняя абсолютная погрешность будет меньше, например, áDХñ = 0,0148, то результат измерений нужно записать так:
X = 2,326 ± 0,015.
9. Точность измерения характеризуется относительной погрешностьюe, и выражается обычно в процентах:
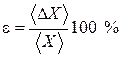 . .
| (6) |
После вычисления значение e нужно обязательно округлить до одной-двух значащих цифр. Например, 1,473 % надо округлить до 1,5 %, а 3,7 % – до 4 %. Для приведённых в п. 8 примеров расчёт относительных погрешностей даёт:
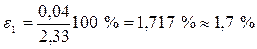 .
. 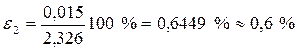 .
.
Полезно знать, что число, записанное с одной значащей цифрой, имеет относительную погрешность около 10 %; с двумя значащими цифрами – около 1 %; с тремя значащими цифрами – около 0,1 %.
Дата добавления: 2015-02-07; просмотров: 1011;
