Погрешности косвенных измерений. Если искомая величина y вычисляется по результатам измерений нескольких величин x1, x2, x3: y = f (x1
Если искомая величина y вычисляется по результатам измерений нескольких величин x1, x2, x3: y = f (x1, x2, x3), то её абсолютную погрешность Dy можно найти, применяя операцию дифференцирования:
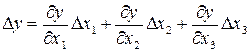 , ,
| (8) |
где Dxi – абсолютная погрешность измеряемой величины xi.
Например, для величины у = 3х2, абсолютная погрешность будет в 6x раз больше, чем для величины x, полученной прямыми измерениями:
| Dу = (3х2)'Dx = 6xDx. | (9) |
Относительная погрешность расчётной величины у для этого случая
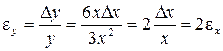 , ,
| (10) |
т.е. в два раза больше, чем относительная погрешность величины х.
Ещё пример: с = 3а2+b3; Dс = 6аDа + 3b2Db.
Приведём таблицу погрешностей (табл. 3) наиболее часто встречающихся функций.
Таблица 3
| № п/п | Функция | Абсолютная погрешность | Относительная погрешность |
| c = A ± B | Dc = DA +DB | eс = 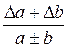
| |
| c = AB | Dc = ADA + BDB | eс = 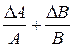
| |
c = 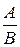
| Dc = 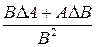
| eс = 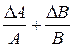
| |
| c = A n | Dc = n (A n – 1)DA | eс = n 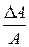
| |
c = 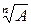
| Dc = 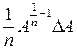
| eс = 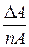
| |
| c = sin A | Dc = (cos A)DA | eс = (ctg A)DA | |
| c = ln A | Dc = 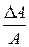
| eс = 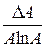
|
Пример из лабораторной работы «Определение показателя адиабаты методом Клемана – Дезорма». Показатель адиабаты g здесь определяется по формуле
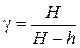 , ,
| (11) |
где величины H и h определяются прямыми измерениями с приборной погрешностью DH = Dh = 1 мм. Пусть при измерениях получили значения H = 202 мм, h = 56 мм. Относительную погрешность величины g определяем по табл. 3, 3-я строка:
eg = 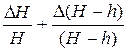 . .
| (12) |
Абсолютную погрешность разности D(H – h) = DH + Dh находим в 1-й строке табл. 3. В итоге
eg = 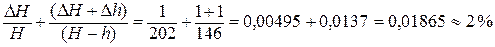 . .
| (13) |
Абсолютную погрешность найдём, умножив значение g= 202/146 = 1,38 на относительную погрешность: Dg = 1,38×0,02 » 0,03. Результат измерений в этом случае следует записать в виде
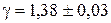 . .
| (14) |
Дата добавления: 2015-02-07; просмотров: 1184;
