Правила действий с приближёнными числами
1. Все результаты измерений являются приближёнными числами. Например, при измерении ширины тетради сантиметровой линейкой получилось приблизительно 17 см, а при измерении линейкой с миллиметровыми делениями – 16,7 см. Оба числа – приближённые, т.е. указывающие ширину тетради с точностью, которая задаётся измерительным прибором.
2. Точность приближённого числа определяется числом значащих цифр,выражающих это число.
3. Значащимисчитаются все цифры числа, кроме нулей, стоящих впередипервой цифры,не равной нулю(т.е. слева от неё), а также нулей, определяющих порядокчисла.
Примеры:
| Одна значащая цифра | Две значащие цифры | Три значащие цифры |
| 0,0004 = 4×10–4 4000 = 4∙103 | 0, 043 = 43∙10–3 4300 = 4,3×103 | 10,5 0,00105 = 1,05×10–3 105 000 = 1,05×105 |
Внимание! Не надо путать число значащих цифр с числом знаков после запятой – это глубоко укоренившееся заблуждение!
4. Результат любого арифметического действия с приближёнными числами нужно округлитьдо той точности (того же числа значащих цифр), какую имели исходные числа. В промежуточных вычислениях допускается одна запасная цифра. Правила округления – общепринятые.
Примеры: 23:14 = 1,6; 23:14×5,87 = 1,64×5,87 = 9,6(3);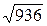 
= 30,6 (а калькулятор показывает = 30,59411708…).
Дата добавления: 2015-02-07; просмотров: 936;