Спецификация и оценивание МНК эконометрических моделей нелинейных по переменным.

Более простым является класс нелинейных переменных, в которых имеется нелинейность, но которые остаются линейными по входящим в них и подлежащих оценке параметрам. Сюда входят полиномы различной степени и равносторонняя гипербола. Такая нелинейная регрессия по включённым переменным в объяснение переменных простым их преобразованием (заменой) легко сводится к обычной линейной регрессии для новых переменных. Поэтому оценка параметров в этом случае выполняется просто по МНК, поскольку зависимости линейны по параметрам.

Так, важную роль в экономике играет нелинейная зависимость, описанная равносторонней гиперболой (1):

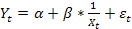. (1)

Произведём замену переменных: обозначим 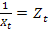. В результате получается линейная модель:

(2)

Её параметры хорошо оцениваются по МНК, и сама зависимость характеризует связь удельных расходов сырья, топлива, материалов с объёмом выпускаемой продукции, временем обращения товаров и всех этих факторов с величиной товарооборота.

В общем случае парабола второй степени, так же как и полиномы более высокого порядка, при линеаризации принимают вид уравнения множественной регрессии:

парабола второй степени 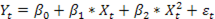. (3)

Применим метод замены переменных: 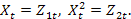После преобразования получается линейная модель:

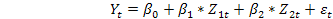(4)

Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.