Аналитический метод построения математических моделей
В распоряжении исследователя, решающего на основе моделирования конкретную задачу, сегодня находится огромное множество моделей-«заготовок», которые могут и должны быть использованы. Все эти заготовки получены на основе универсальных законов, таких, как закон сохранения вещества и энергии, начала термодинамики, закон всемирного тяготения. Однако вопрос о том, каким может быть удельный вес теоретической составляющей при построении каждой конкретной модели, целиком определяется требованиями задачи и характером объекта моделирования.
Возможность и рациональность теоретического подхода к моделированию некоторого объекта определяются целым рядом практически не поддающихся формальному анализу факторов, к числу которых относятся:
степень изученности данного класса объектов и наличие теоретической базы, достаточной для модельного описания объекта в соответствии с требованиями решаемой задачи;
приемлемость ограничений и допущений, содержащихся в исходных теоретических построениях, применительно к условиям и требованиям решаемой задачи;
специфические свойства объекта-оригинала (степень сложности и размерность модели, возможность линеаризации, возможность и удобство применения стандартных, например частотных, методов для исследования модели объекта и т. п.);
возможность и удобство введения в теоретическую модель необходимой дополнительной информации, получаемой опытным путем;
возможность экспериментального исследования объекта-ориги-нала.
В основе аналитических моделей, как правило, лежат балансовые соотношения, связывающие входные и выходные переменные. Эти соотношения представляют собой частные проявления законов сохранения вещества и энергии.
Пример 1. В простейшей ЭЭС генератор электрической станции Г (рис. 4.2) работает с мощностью PГ, которая посредством линии электропередачи передается на шины нагрузки, где установлен электродвигатель Д.
В такой ЭЭС при неизменной частоте сохраняется баланс активной мощности:
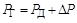 ,
,
где Pд – мощность, с которой работает электродвигатель;
DP – потери мощности в линии электропередачи.
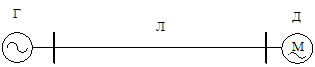
Рис. 4.2. Схема простейшей ЭЭС
Выражение (4.1) является балансовым соотношением, вытекающим из закона сохранения энергии, однако для полного описания модели работы ЭЭС требуются дополнительные экспериментальные данные. К ним относятся характеристики элементов, входящих в ЭЭС: генератора, линии электропередачи и двигателя. Эти элементы являются техническими объектами со своими, свойственными только им, характеристиками. Для получения этих характеристик требуется эксперимент, который проводится непосредственно для этих объектов, либо используются данные экспериментов, выполненные над типичными объектами. К характеристикам электрических объектов относятся, например, статические характеристики генераторов и двигателей по напряжению, а для линии электропередачи – зависимость потерь мощности от напряжения.
Пример 2. При протекании тока по проводу воздушной ЛЭП в соответствии с законом Джоуля–Ленца происходит нагревание проводника:
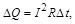
где ΔQ – количество теплоты, выделяемое в проводнике с сопротивлением R при протекании по нему тока I в течение времени Δt.
Если бы не было отвода тепла от проводника, температура проводника возрастала бы неограниченно. Охлаждение проводника происходит лучеиспусканием, конвекцией и теплопередачей из-за наличия теплопроводности окружающей среды.
По условиям сохранения физико-механических характеристик проводов воздушных линий электропередачи температура, до которой могут нагреваться провода, ограничена некоторым значением (как правило 70 ºС). Это связано с ограничением тока, протекающего по проводу Iдоп. Вычислить значение Iдоп позволяет математическое соотношение, выведенное из баланса количества теплоты, создаваемого в отрезке проводника, и отведенного количества теплоты в единицу времени.
Лучеиспускание при θ < 100 ºС незначительно, а теплопроводность окружающего проводник воздуха мала, следовательно, в основном охлаждение идет за счет конвекции воздуха:
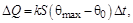
где S – поверхность проводника;
θmax и θ0 – максимальная и начальная температура провода;
k – коэффициент пропорциональности.
Приравняем количество создаваемой и количество отводимой теплоты, получим
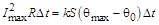 ,
,
откуда
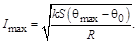
Дата добавления: 2015-03-20; просмотров: 2165;
