Обобщенный закон трения
Все реальные жидкости и газы обладают вязкостью, т.е. оказывают сопротивление смещению одних частиц относительно других. Результатом этого является возникновение в них наряду с нормальными напряжениями также и касательных напряжений. Интенсивность смещения частиц характеризуется скоростью деформации. Поэтому логично установить связь между напряжениями в движущейся жидкости и характеристикой ее деформационного движения.
 Предположим, что вектор напряжений
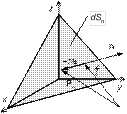
Предположим, что вектор напряжений 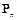 , действующих на площадке dS, ориентированной в соответствии с вектором
, действующих на площадке dS, ориентированной в соответствии с вектором 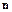 , можно представить в виде суммы двух векторов:
, можно представить в виде суммы двух векторов:
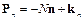 , (1.10)
, (1.10)
где 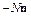 – вектор, действующий по нормали к площадке, значение которого определяется скалярной величиной N;
– вектор, действующий по нормали к площадке, значение которого определяется скалярной величиной N; 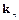 – вектор, обусловленный только вязкостью.
– вектор, обусловленный только вязкостью.
Представим вектор напряжений, зависящий от вязкости в виде
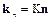 ,
,
где 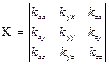 – тензор напряжений, обусловленных вязкостью.
– тензор напряжений, обусловленных вязкостью.
Тогда уравнение (1.10) примет вид
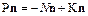 . (1.11)
. (1.11)
Для широкого класса жидкостей («ньютоновских» жидкостей) экспериментально установлено наличие линейной связи между тензором напряжений, зависящим от вязкости, и тензором скоростей деформаций
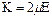 (1.12)
(1.12)
или
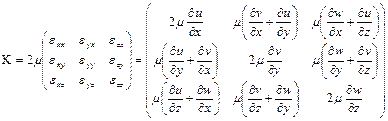 .
.
Уравнение (1.12) называют обобщенным законом трения.
Представим скалярную величину N в виде матрицы, умножив ее на единичную матрицу 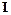 (тензорную единицу)
(тензорную единицу)
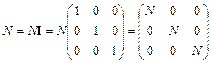 .
.
Тогда матричная форма уравнения (1.11) будет иметь вид
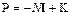
или
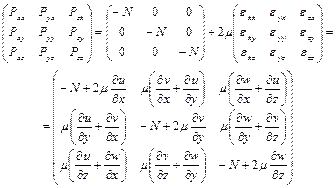
Среднее арифметическое нормальных напряжений, действующих на трех взаимно-перпендикулярных площадках, проходящих через одну точку и расположенных в координатных плоскостях, взятое с обратным знаком, считают гидродинамическим давлением p в этой точке
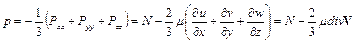 . (1.13)
. (1.13)
Из данного уравнения следует, что формально введенная скалярная величина N определяется гидродинамическим давлением, вязкостью и скоростью потока жидкости
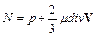 .
.
На основании материала, изложенного выше, вектор напряжений, действующий на произвольной площадке, ориентация которой в пространстве задана, определяется уравнением
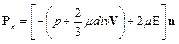 , (1.14)
, (1.14)
которое устанавливают зависимость его от гидродинамического давления, вязкости жидкости и скоростями ее деформации.
Дата добавления: 2015-01-24; просмотров: 778;
