Уравнение неразрывности. Выше упоминалось, что в гидравлике рассматриваются жидкости, обладающие свойством сплошности, которое предполагает непрерывность изменения параметров потока и

Выше упоминалось, что в гидравлике рассматриваются жидкости, обладающие свойством сплошности, которое предполагает непрерывность изменения параметров потока и их производных в пространстве и времени.

Уравнение неразрывности выведем из закона сохранения массы: масса изолированной системы не меняется с течением времени. Следовательно, полная производная массы по времени равна нулю.

Выделим в жидкости бесконечно малый объем 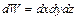, масса которого 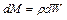, и применим к нему закон сохранения массы

После деления левой и правой частей уравнения на объем и проведения элементарных преобразований получим

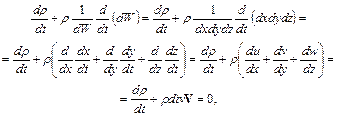
где 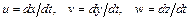– проекции вектора скорости 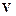на оси координат.

Раскрыв в последнем уравнении полную производную плотности по времени, получим окончательный результат

. (1.7)

Для несжимаемой жидкости, плотность которой не меняется, уравнение неразрывности примет вид:

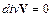. (1.8)

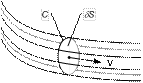Проанализируем установившийся поток жидкости, в каждой точке которого вектор скорости не меняется с течением времени. Для анализа полезно ввести линии в области течения, касательные к вектору скорости в каждой точке потока. Такие линии называют линиями тока.

Рассмотрим замкнутую кривую (контур) С, проведенную вокруг точки в потоке жидкости и охватывающую элементарную площадку dS, которая расположена в плоскости, перпендикулярной вектору скорости рассматриваемой точки. Линии тока, проходящие через контур, образуют замкнутую поверхность – трубку тока. Жидкость, находящаяся внутри трубки тока, называется струйкой.

Поскольку, по определению, не существует компоненты вектора скорости, нормальной к линиям тока, ни одна частица жидкости не пересечет поверхность трубки тока. Следовательно, массовый расход жидкости вдоль трубки тока остается постоянным, т.е.

,

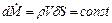где r – плотность жидкости; V – скорость жидкости вдоль трубки тока.

Так как для капельных жидкостей r практически остается постоянной, то остается постоянным и объемный расход жидкости dQ вдоль трубки тока

.

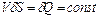Полный объемный расход через всю площадь течения S, в пределах которой скорость остается постоянной, равен

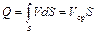. (1.9)

Уравнение (1.9) используют для определения расхода жидкостей, движущихся по каналам и трубопроводам.