Уравнение движения жидкости

Выделим в потоке произвольный объем жидкости W, ограниченный поверхностью S, и запишем для него закон изменения количества движения: производная по времени от главного вектора количества движения системы, состоящей из частиц жидкости, находящихся в выделенном объеме, равна главному вектору приложенных к ней внешних сил, или

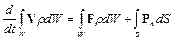. (1.15)

Преобразуем данное уравнение:

поменяем местами знаки дифференцирования и интегрирования в левой части уравнения и распишем дифференциал произведения. Кроме того, принимая во внимание уравнения неразрывности 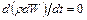, получим

;

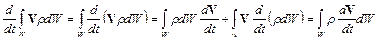с помощью формулы Остроградского-Гауса интеграл по поверхности от потока вектора можно преобразовать в интеграл по объему от дивергенции этого же вектора, т.е.

,

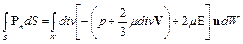который с помощью оператора Гамильтона и принятые в векторном анализе формальные преобразования (см. приложение), преобразуется к виду

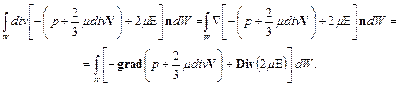
Подставляя в уравнение (1.15) преобразованные выражения, после выполнения элементарных операций получим

.

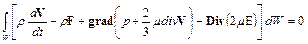Данное выражение справедливо при равенстве нулю подынтегрального выражения, следовательно

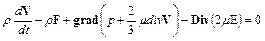
или

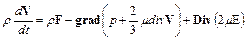. (1.16)

Проекции уравнения (1.16) на оси координат имеют вид

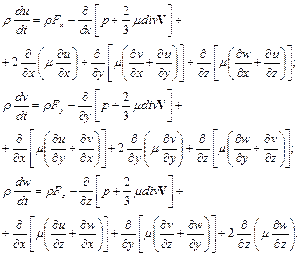(1.17)

Уравнения (1.16) и (1.17) называют уравнениями Навье-Стокса. Они является основой гидромеханики и газовой динамики. Их используют для исследования движения вязких сжимаемых жидкостей и газов. В зависимости от способа решения или упрощения этих уравнений механика жидкости и газа разделяется на следующие разделы:

гидростатику, где изучают явления, происходящие в неподвижной жидкости ( );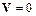

динамику идеальной (невязкой) жидкости, т.е. жидкости, у которой ;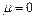

динамику несжимаемой жидкости, т.е. жидкости, у которой постоянная плотность ( );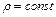

газовую динамику или динамику вязкой, сжимаемой жидкости.

Поскольку уравнения Навье-Стокса содержат шесть неизвестных величин (u, v, w, r, m, p), то для замыкания системы их дополняют:

уравнением неразрывности ,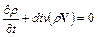

уравнением состояния ,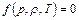

зависимостью вязкости от температуры .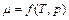

Появление дополнительной переменной – температуры T, требует введения еще одного уравнения – уравнения баланса энергий, которое имеет следующую формулировку: производная по времени от полной энергии движущегося объема среды равна сумме мощностей приложенных к объему внешних сил, а также подводимой к нему за единицу времени внешней энергии

.

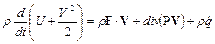Дифференциальные уравнения имеют бесчисленное множество решений. Для выбора единственного решения, соответствующего рассматриваемой задаче, данную систему необходимо дополнить условиями однозначности – математическим описанием частных особенностей конкретной задачи.

Условия однозначности включают:

геометрические условия, которые служат для описания формы и размеров системы;

физические условия, служащие для задания физических свойств среды;

граничные условия, в которых описывают особенности протекания процессов на границах системы;

временные условия, определяющие особенности протекания процессов во времени.

Вопрос о существовании и единственности решения полной системы уравнений движения до настоящего времени не решен. Однако полученные частные решения хорошо подтверждаются экспериментальными исследованиями, из чего делают вывод об адекватности приведенных выше уравнений реальным гидродинамическим процессам.

Из уравнений Навье-Стокса получены критерии подобия гидродинамических процессов, которые позволяют с помощью теории подобия обобщать многочисленные экспериментальные исследования.