Производная по направлению. Градиент

Рассмотрим функцию z = f(M), определенную в некоторой окрестности точки M(x;y), и произвольный единичный вектор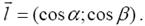

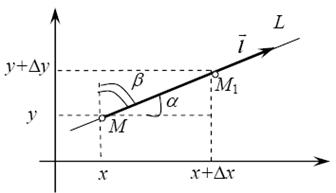
Проведем в направлении вектора l прямую MM1. Точка M1 имеет коор­динаты (x + Dx; y + Dy). Величина отрезка MM1 равна

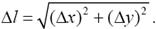
Функция f(M) при этом получит

приращение:

Dz = f(x + Dx; y + Dy) - f(x; y)

Предел отношения 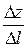при

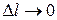
(M ®M1 ), если он существует и ко­нечен, называеlтся производной функции z = f(M) в точке M(x;y) по направлению вектора l и обозначается 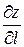, т.е. .

При нахождении производной по направлению пользуются формулой:

(1)

Градиентом функции z = f(M) в точке M(x;y) называется вектор, коор­ди­наты которого равны соответствующим частным производным 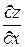и 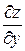, взятым в точке M(x; y). Обозначается:

(2)

Учитывая определение градиента, формулу (1) можно представить в виде скалярного произведения двух векторов:

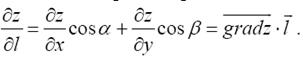(3)

Аналогично определяется производная по направлению и градиент функ­ции трех переменных u = f(x; y; z):

.

Градиент функции характеризует направление, а его модуль величину наибыстрейшего роста функции в данной точке (наибольшую скорость изме­нения функции в точке). Понятия производной по направлению и градиента функции играют важную роль во многих приложениях.