Полный дифференциал сложной функции
Найдем полный дифференциал сложной функции, определяемой равенствами (7) и (8). По формулк (4)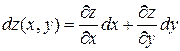 
, а частные производные 
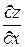и 
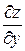сложной функции определяются равенствами (11) и (12) соответственно. Следовательно
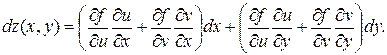
Преобразуем правую часть
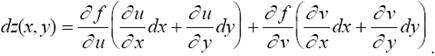
Так как
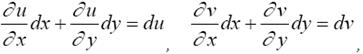
то последнее равенство примет вид
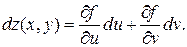(13)
Сравнивая формулы (13) и (4), можно сказать, что полный дифференциал функции z = f(u, v) имеет один и тотже вид независимо от того, являются ли ее аргументы независимыми переменными или функциями независимых переменных. Этот факт называют свойством инвариантности дифференциала первого порядка. Таким образом, установлено, что функции нескольких переменных обладают свойством инвариантности формы первого дифференциала.
Дата добавления: 2015-01-24; просмотров: 1703;