Частные производные высших порядков

Определение 4Частная производная (если она существует) от частной производной первого порядка функции z = f(x,y) называется частной произ­водной второго порядка.

Дифференцируя f ′x(x, y) по х и по у, получим две частные производные второго порядка, которые обозначаются следующим образом:

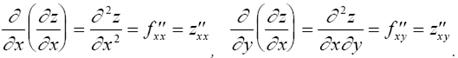
Аналогично для f ′y(x, y):

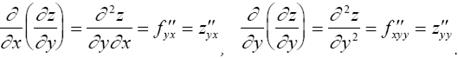
Производные f ′′xy(x, y) и f ′′yx(x, y) называются смешанными производ­ными, они отличаются тем, что первая получена дифференцированием функции z снача­ло по x, а затем по y, а вторыя наоборот, - сначало по y, а затем по x. При этом справедлива следующая

Теорема 6 (о равенстве смешанных производных). Если функция z = f(x, y) и ее производные f ′x, f ′y, f ′′xy, f ′′yx определены и непрерывны в точке P(x, y) и некоторой ее окрестности, то в этой точке справедливо равенство

Производные второго порядка в силу их непрерывности можно снова диф­ференцировать, как по х так и по y, в результате получаем производные третьего порядка и т.д.

Таким образом, частной производной порядка n функции z = f(x, y) называется первая производная от частной производной (n – 1) порядка.

Для частных производ­ных высших порядков справедлива теорема о равенстве смешанных производных, т. е. о независимости результата от порядка дифференцирования, аналогичная теореме 6.