Производная сложной функции. Полная производная

Обобщим понятие сложной функции на случай функции многих переменных. Пусть дана функция

z = f(u, v), (7)

аргументы которой u и v – функции других переменных х и у:

u = ϕ(x, y), v = ψ(x, y). (8)

Если в соотношение (7) вместо u и v подставить их выражения через х и у, то в результате получим сложную функцию переменных х и у:

z = f(u, v) = f(ϕ(x, y),ψ(x, y)) = F(x, y).

В частном случае, если u и v зависят только от одного переменного: u = ϕ(x), v = ψ(x), то сложная функция z = f(u,v) = f(ϕ(x),ψ(x)) = F(x) является функцией одного переменного х.

Рассмотрим правила дифференцирования сложной функции. Имеет место следующая теорема.

Теорема 1.Если z = f(u, v), u = ϕ(x) и v = ψ(x) дифференцируемые функции, то производная 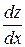существует и равна:

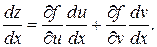(9)

Рассмотрим общий случай. Пусть z = f(u, v), где аргументы u и v зави­сят от двух и более преременных, например, определяются равенствами (8). Тогда z является функцией двух независимых переменных x и y . Для нахож­дения ее частной производной 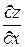зафиксируем y. Поскольку в этом случае z – функция одной переменной x, то применяя формулу (9), получим

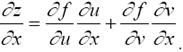(11)

Аналогично находим частную производную z по y:

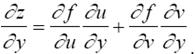(12)