Частные производные

Рассмотрим функцию двух переменных z = f(x,y), заданную в некоторой области D. Если зафиксируем одну из переменных, например, положив у = у0, то получим функцию z = f(x, y0) только одной переменной х. Можно поставить вопрос о вычислении ее производной в точке х = х0 . Дадим значению аргумента х0 приращение Δх, тогда функция получит приращение, которое будем называть частным приращением (в связи с тем, что оно соответствует изменению только одного аргумента) функции z = f(x, y) по аргументу х и обозначать:

Δх z = Δх f(x0, y0) = f(x0 +Δx, y0) - f(x0, y0).

По определению производной для функции одной переменой z = f(x, y0) имеем

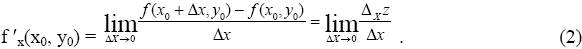
Для функции двух переменных z = f(x,y) предел (2) называется частной производной по х в точке (x0, y0) и обозначается одним из следующих способов:

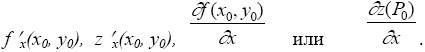
Таким образом, приходим к следующему определению частной произ­водной.

Определение 1. Частной производной функции z = f(x, y) по переменной х называется предел отношения соответствующего частного приращения функции к приращению аргумента х при условии, что приращение аргумента стремится к нулю произвольным образом, т. е.

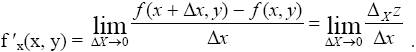
Если предел (2) существует, то частная производная функции z = f(x,y) по х в точке Р0 (x0, y0) имеет вполне определенное значение. При этом в различных точках плоскости она принимает, вообще говоря, различные значения. Таким образом, частная производная по х сама является функцией двух переменных, которая определена во всех точках плоскости, где существует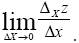

Аналогично определяют и обозначают частное приращение и частную производную функции z = f(x,y) по аргументу у:

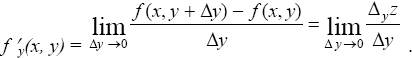
Частная производная по х (у) выражает скорость изменения функции в данной точке в положительном направлении оси Ох (Оу).

Определение частного приращения и частной производной переносится на функции любого конечного числа переменных. Например, частная производная по переменной хk ( 1≤ k ≤ n) для y = f(P), где Р(х1, х2, ..., хn), определяется равенством:

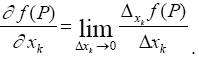
При нахождении частной производной применимы все формулы и правила дифференцирования функции одной переменной, так как по определению мы фиксируем все переменные, кроме одной, и фактически имеем дело с функцией одной переменой. Если, например, находим производную по х, то все остальные аргументы рассматриваем как константы.

Пример 1. Найти частные производные функции z(x, y) = x²– 2y.

Решение. При нахождении 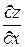считаем, что у – константа, а х – переменная величина, поэтому 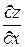= (x²– 2y)′x= (x²)′x – (2y)′x = 2x. Аналогично, 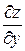=( x²– 2y)′у= = (x²)′у – (2y)′у = – 2.