Предел и непрерывность

Определение 4 .Круг радиуса δ с центром в точке Р0 называется δ-окрестностью точки Р0 .

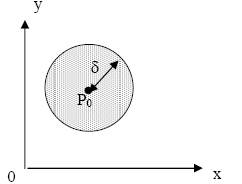Из этого определения следует, что δ-окрестность точки Р0(х0,у0) есть множество точек плоскости, удаленных от точки Р0 на расстояние, меньшее δ (рис. 6). Таким образом, координаты произвольной точки Р(х,у) из данной окрестности удовлетворяют неравен­ству

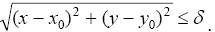
Рис. 6

Сформулируем определение предела функции двух переменных.

Определение 5. Число А называется пределом функции f(x, y) в точке Р0 (х0, у0) ( при стремлении точки Р(х, у) к точке Р0 (х0,у0)), если для любого числа ε > 0 найдется такое число δ = δ(ε) > 0, что | f(P) − A | < ε для всех Р(х, у) из δ-окрестности точки Р0.

Обозначение:

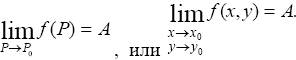
Геометрически это означает следующее. Рассмотрим на плоскости Оху переменную точку Р(х,у). Наблюдая на графике за изменением соответствующей аппликаты z = f(P), будем приближать Р к точке Р0 по некоторому произвольному пути. Как только расстояние от точки Р до Р0 станет меньше, чем δ, аппликата соответствующей точки графика будет отличаться от числа А меньше, чем на ε. Поскольку ε – произвольное число, то значения функции f(P) могут быть как угодно близки к числу А. При этом число δ определяется заданием ε , т. е. зависит от ε (δ = δ(ε)).

На функции двух переменных легко переносятся все положения теории пределов функции одной переменной. В частности, для функций f(P) и g(P), которые имеет предел в точке Р0, справедливо:

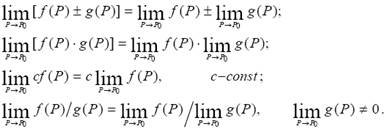
При вычислении пределов функций нескольких переменных можно использовать известные для функций одной переменной приемы раскрытия неопределенностей. В частности, замечательные пределы:

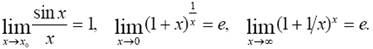
Определение 6.Функция z = f(x,y) называется непрерывной в точке Р0 (х0,у0), если она определена в точке Р0(х0,у0) и некоторой ее окрестности и

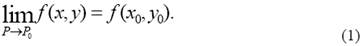
Если в некоторой точке Р0 (х0,у0) не выполняется условие (1), то точка Р0 (х0,у0) называется точкой разрыва функции z = f(x,y). Разрыв в точке Р0 может произойти по следующим причинам:

1) если функция определена в некоторой окрестности точки Р0 , но не определена в самой этой точке;

2) если функция определена в точке Р0 и ее окрестности и не имеет предела при стремлении точки Р к Р0;

3) если функция, определенная в точке Р0 и ее окрестности, имеет предел в точке Р0, отличный от значения функции в этой точке.

Для функции нескольких переменных, как и для функции одной переменной, справедлива следующая теорема.

Теорема 1.Если функции z = f(M) и z = g(M) непрерывны в точке Р0 , то функции f(M) ± g(M), f(M)⋅g(M), f(M)/g(M) (при условии g(Р0) ≠ 0) непрерывны в точке Р0.

Функция называется непрерывной в области, если она непрерывна в каждой точке этой области.

1.4. Замечание о функциях n (n>2) переменных

Обобщая понятие функции двух переменных, сформулируем определение функции любого конечного числа переменных.

Определение 7.Если упорядоченному набору n действительных чисел (х1, х2, ..., хn) по определенному правилу или закону (обозначим его символом f ) единственным образом соответствует действительное число у, то говорят, что у является функцией n переменных и пишут у = f(х1, х2, ..., хn).

Наборы (х1, х2, ..., хn) принято называть точками n-мерного пространства и обозначать Р(х1, х2 , ... , хn), а у = f(х1, х2, ..., хn) = f(Р). Принимая это во внимание, можно дословно переносить все определения для функции двух переменных на функции произвольного числа переменных. Например, областью определения функции у = f(х1, х2, ..., хn) = f(Р), (n ≥ 2) называется множество всех тех точек Р n-мерного пространства, для которых функция определена, а графиком – множество точек (х1, х2, ..., хn, f(Р))(n+1)-мерного пространства. При n>2 функция y = f(Р) не имеет геометрического истолкования, хотя при n = 3 область определения у = f(Р) представляет собой некоторое множество точек трехмерного пространства.

Пример 12. Найти область определения функции u(x,y,z)= ln(4-x²- y² - z²).

Решение. Логарифмическая функция определена только для положительных аргументов. Следовательно, область определения функции u(x, y, z) задается неравенством 4 – x²– y² – z² > 0 или x² + y² + z² < 4. Последнему неравенству удовлетворяют координаты всех точек, которые находятся внутри сферы радиуса 2 с центром в точке (0,0,0,).