Дифференциальное исчисление функций многих переменных

2.1. Вычисление объема тела по известным площадям параллельных сечений. Если известны площади сечений тела плоскостями, перпендикуляр­ными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела 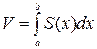в предположении, что S(x) − интегрируемая функция.

2.2. Вычисление объема тела вращения:

а) если тело образовано вращением криволинейной трапеции, ограни­чен­ной кривой y = f(x), осью OX и двумя прямыми x = a и x = b(a < b) вокруг оси OX, то объем тела

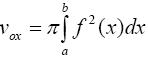
б) если тело образовано вращением фигуры, ограниченной кривой

x = j(y) , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем

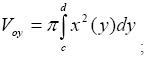
в) если тело образовано вращением вокруг оси OY фигуры, ограничен­ной линией y = f (x), прямыми x = a, x = b (0 ≤ a ≤ b) и осью OX, то его объем можно вычислить по формуле

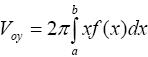
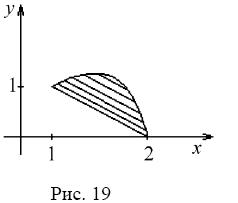
П р и м е р. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций y = 2x − x² и y = 2 − x вокруг оси OX.

Решение. Найдем точки пересечения параболы y = 2x − x² и прямой y = 2 − x . Решим систему:

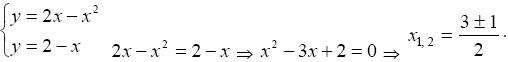
Получим две точки пересечения: х₁ = 1, у₁ = 1; х₂ = 2, у₂ = 0. Сделаем чертеж (рис. 19).

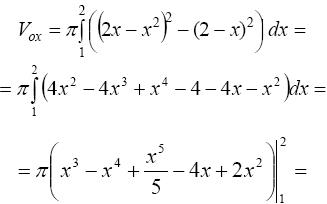
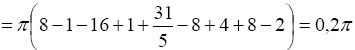
П р и м е р. Вычислить объем тела, ограни­чен­ного поверхностями:

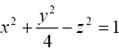; z = 0; z = 3.

Решение.

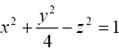− однополостной гипербо­лоид. При пересечении его плоскостями z = h в сечении получаем эллипсы

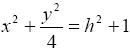
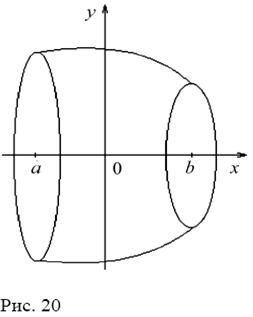
(рис. 20) с полуосями

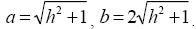
Как известно, площадь эллипса S =πab, тогда S(h) = 2π(h² +1) 0 ≤ h ≤ 3

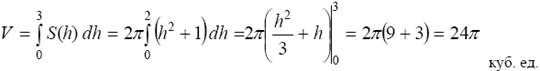
Дифференциальное исчисление функций многих переменных