Полное приращение и полный дифференциал
Пусть Р(х, у) и Р1(х1, у1) – точки области D, в которой задана функция z=f(x, y). Найдем изменение функции при переходе из точки Р в точку Р1. Разность значений функции в точках Р и Р1 называется полным приращением функции z = f(x, y) в точке Р и обозначается Δz(x, y) или Δf(P):
Δz(x,y) = Δf(P) = f(P1) − f(P) = f(x1, y1) − f(x,y).
Обозначим приращение аргументов х и у при переходе из точки Р в точку Р1 через Δх и Δу: Δх = х1 − х, Δу = у1 − у. Следовательно,
Δz(x,y) = f(x + Δx, y + Δy) − f(x,y).
Геометрически эта разность дает приращение аппликаты графика функции z = f(x, y) при переходе из точки Р в точку Р1. Используя понятие полного приращения функции, можно дать определение непрерывности функции в точке, равносильное данному ранее определению 6.
Теорема 1.Для того, чтобы функция z = f(x, y) была непрерывна в точке Р0(х0,у0), необходимо и достаточно, чтобы полное приращение функции Δz(P0) стремилось к нулю при Δx и Δy, стремящихся к нулю.
Определение 2.Функция z = f(x, y) называется дифференцируемой в точке Р(х, у), если ее полное приращение Δz(Р) можно представить в виде :
Δz(Р) = АΔx + ВΔy + γ, (3)
где А и В не зависят от Δx и Δy, а γ = γ (х, у, Δx, Δy) - бесконечно малая величина более высокого порядка малости, чем ρ =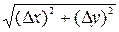 
при ρ → 0.
Таким образом, полное приращение дифференцируемой функции представимо в виде двух слагаемых, одно из них (АΔx + ВΔy) линейно зависит от Δx и Δy, а другое (γ ) – мало′ по сравнению с ρ (γ=о(ρ)) при ρ → 0. Отметим, что ρ равно расстоянию между точками Р1 и Р , поэтому условие ρ → 0 (Δx→ 0 и Δу→ 0 одновременно) равносильно условию Р1 → Р .
Слагаемое АΔx + ВΔy в (3) при ρ ≠ 0 составляет главную часть полного приращения функции и, как отмечалось выше, линейно зависит от Δx, Δy. Выражение АΔx+ВΔy называется полным дифференциалом функции z = f(x, y) и обозначается dz или df(x, y). В случае ρ = 0 полагают dz = 0.
Определение 3. Полным дифференциалом функции z = f(x, y) называется главная часть полного приращения функции, линейная относительно Δx и Δy, т. е.
df(x, y) = АΔx + ВΔy.
Из равенства (3) и теоремы 1 следует, что всякая дифференцируемая функция непрерывна.
Кроме того, из условия дифференцируемости функции в точке следует, что в данной точке существует полный дифференциал. Следующая теорема устанавливает связь между понятием дифференцируемости (дифференциалом) и частными производными.
Теорема 2.Если функция z = f(x, y) дифференцируема в точке Р(х, у), то в этой точке существуют частные производные z′x , z′y и справедливо равенство :
dz(x, y) = z′x Δx + z′y Δy . (4)
Отметим, что, в отличие от функции одной переменной, обратная теорема неверна: из существования частных производных еще не следует дифференцируемость функции. Однако если предположить, что частные производные не только существуют, но и непрерывны, то функция будет дифференцируемой. Справедлива следующая теорема.
Теорема 3.Если функция z = f(x, y) имеет частные производные в некоторой окрестности точки Р(х, у), которые непрерывны в точке Р(х, у), то полное приращение представимо в следующем виде:
Δf(Р) = f ′x Δx + f ′y Δy + αΔx + βΔy,
где α и β стремятся к нулю при Δх → 0 и Δу → 0.
Легко показать, что γ = α Δх + β Δу = ο( 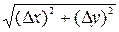),следовательно, теорема 3 дает достаточное условие дифференцируемости функции в точке.
Приращения Δх и Δу независимых переменных х и у функции z = f(x, y) (как и в случае функции одной перерменной) будем называть их дифференциалами обозначать dx и dу, соответственно. Тогда согласно формуле (4) выражение полного дифференциала примет вид:
dz = f ′x dx + f ′y dy или dz =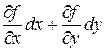 
. (5)
В отличие от полного дифференциала функции z = f(x, y) выражения dxz =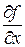 
dx и dyz = 
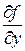dy называют частными дифференциалами этой функции.
Предыдущие рассуждения и определения соответствующим образом обобщаются на функции любого конечного числа переменных. Например, полный дифференциал функции f(х1, х2, ..., хn) определяется равенством:
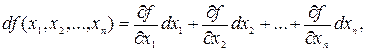
т. е. равен сумме частных дифференциалов по всем переменным.
Все известные правила нахождения дифференциалов остаются справедливыми для функций нескольких переменных. В частности, для любых дифференцируемых функций u = u(P) и v = v(P) и константы с справедливы следующие формулы:
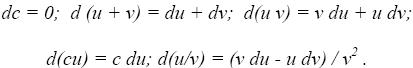
Дата добавления: 2015-01-24; просмотров: 5149;