Функции двух переменных.

Понятие функции одной переменной не охватывает все зависимости, существующие в природе. Даже в самых простых задачах встречаются величины, значения которых определяются совокупностью значений нескольких величин.

Пример 1. Площадь S прямоугольника со сторонами, длины которых равны х и у, выражается формулой S = xy, т.е. значение S определяется совокупностью значений х и у.

Пример 2. Объем V прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z, выражается формулой V = xyz, т. е. значение V определяется совокупностью значений x, y и z.

Математической моделью подобных зависимостей является понятие функции нескольких переменных.

Определение 1.Переменная z называется функцией двух переменных x и y , если по некоторому вполне определенному закону упорядоченным парам чисел (x, y) из некоторого множества D ставится в соответствие вполне определенное значение z.

Тот факт, что переменная z является функцией переменных х и у, обозначается так: z = f(x,y) или z = g(x,y) и т.д., при этом буквой f (или g) символически обозначают то правило, по которому данной паре чисел (х, у) ставится в соответствие число z. Переменные х и у называются независимыми переменными или аргументами. Если паре чисел (х0,у0) соответствует число z0, то оно называется значением функции z = f(x,y) и обозначается z0 = f(х0,у0). Поскольку пару действительных чисел (x,y) можно рассматривать как декартовы координаты некоторой точки Р плоскости Оху, то о функции z = f(x,y) часто говорят, что z есть функция точки Р(x,y) и пишут z = f(Р).

Функция z = f(x,y) может быть задана аналитически (формулой) или каким-либо иным способом: например, в виде таблицы, в виде какой-либо словесной формулировки, графически и т. д.

Определение 2.Множество пар (х,у), для которых определено значение z функции z = f(x,y), называется областью определения данной функции.

Область определения функции, заданной явно с помощью формулы, определяется самой формулой.

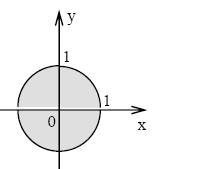
Пример 3. Найти область определения функции z = ln(1 - x² - y²).

Решение. Логарифмическая функция определена только для положительных аргу­мен­тов, поэтому x2 + y2 < 1. Последнее нера­венство задает область определения данной функции. На плоскости Оху ему соответствует внутренность круга радиуса 1 с центром в начале координат.