Вертикальный градиент

Для оценки глубины залегания намагниченных источников можно использовать совместный анализ наблюденного магнитного поля и его вертикальной производной. Если измерения выполнены протонным или квантовым магнитометрами, то для диполя можно написать упрощенное выражение

.

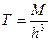Дифференцируя данную формулу, получим

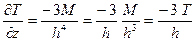. (8.16)

Заметим, что аномалия вертикального градиента от диполя изменяется пропорционально множителю 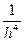, а аномалии полного вектора Т – пропорционально . Получаем, что вертикальный градиент полного вектора Т изменяется с расстоянием намного быстрее самой аномалии наблюденного поля и это его свойство может быть использовано для автоматической локализации магнитных аномалий.

Для тонкого пласта будем иметь аномалию

,

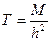вертикальный градиент

. (8.17)

Аномалия градиента от такого источника изменяется пропорционально . По аналогии для любого намагниченного источника можем записать

,

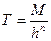аномалия градиента будет равна

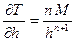. (8.18)

Данные формулы могут быть использованы для быстрого определения глубины залегания источников магнитного поля. Для диполя получим

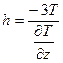, (8.19)

для горизонтального цилиндра –

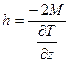, (8.20)

для края узкой вертикальной дайки –

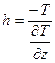(8.21)

и для аномалий в общем случае –

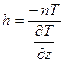. (8.22)

Способ прост, точность его – порядка несколько процентов. На практике он заключается в построении некой функции S, представляющей отношение T_a к вертикальному градиенту ,

. (8.23)

Для определения вертикального градиента можно пользоваться известным интегралом Пуассона по расчету Т_а на высоту Δh. В качестве среднего градиента можно использовать отношение

(T_{a max} – T_{a max}(Dh)) / ∆h.