Логарифмические палетки
При исследованиях на рудных месторождениях магниторазведка обычно применяется в комплексе с электроразведкой. В связи с этим при обработке и интерпретации результатов используются методы, применяемые в электроразведке. По измеренным аномалиям на билогарифмическом бланке‑бумаге строится аномальный график, который накладывается на специальную логарифмическую палетку. При сравнении практической кривой с кривой палетки определяют глубину аномального тела.
Рассмотрим построение палетки на примере вертикального пласта неограниченного распространения в глубину. Согласно формуле
Z = 2 J ( arctg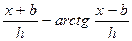 
)
максимальную амплитуду аномалии можно вычислить по формуле
Z max = 2J 2 arctg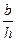 
.
Чтобы исключить зависимость амплитуды от J и b, возьмем отношение Z/Z max. Если обозначить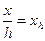 
и 
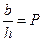, то получим
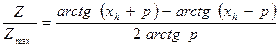. (8.25)
В точке хh=0 это отношение равно единице и его логарифм равен нулю.
Принимая эту точку за начало координат, построим логарифмический график функции Z/Z max (рис.8.13). Совокупность графиков, полученных для различных Р, представляет собой логарифмическую палетку. Индексами графиков являются значения Р. Вертикальная линия при хh=1 служит для определения глубины h.
Пусть по профилю проведены наблюдения с шагом Δх и получены результаты Z0, Z1, Z2, Z3, где Z0 – максимальное значение аномалии. По относительным значениям Z1 / Z0 =1, Z2 / Z0, Z3 / Z0… на билогарифмической бумаге строится график. Этот график накладывается на палетку с теоретическими графиками (масштабы должны быть одинаковыми), и по точке, полученной при пересечении этим графиком вертикальной линии, при xh =1, определяется глубина h.
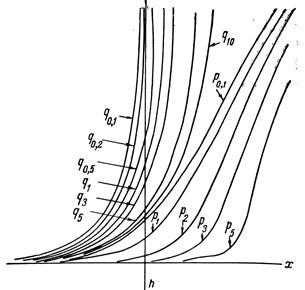
Рис.8.13. Логарифмическая палетка для оценки глубины
намагниченного тела
Логарифмические палетки рассчитаны и построены для оценки количественных параметров аномальных тел при вертикальной и косой намагниченности, вертикальных и наклонных слоев неограниченного распространения. Набор палеток составляет атлас. Для выбора палетки необходимо предположить форму и намагниченность тела. Эти данные могут быть взяты из априорной информации.
Дата добавления: 2015-02-16; просмотров: 1042;