Теорема об оценке. Формула среднего значения
Теорема 1(об оценке определенного интеграла). Если m и M − соответственно наименьшее и наибольшее значения непрерывной функции f(x) на отрезке [a, b], то
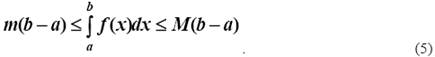
Теорема 2(о среднем значении). Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка С такая, что
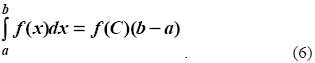
Величина
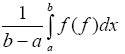
называется средним значением функции f(x) на отрезке [a, b].
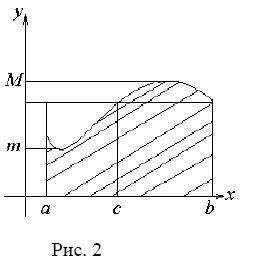
Замечание 1. Теорема 2 имеет четкий геометрический смысл: величина определенного интеграла при f(x) ≥ 0 равна площади прямоугольника, имеющего высоту f(C) и основание (b − a)(рис. 2).
Имеют место более общие теоремы об оценке и среднем: если функции f(x) и φ(x) непрерывны на отрезке [a, b] и φ(x) > 0, m − наименьшее, M − наибольшее значения функции f(x), то
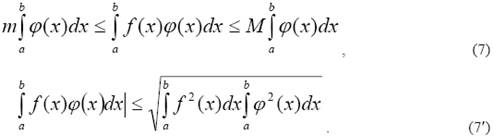
Из соотношений (7) и (7′) следуют соотношения (5) и (6), если принять φ(x) ≡ 1. Для непрерывных на отрезке [a, b] функций f(x) и φ(x) имеет место неравенство Коши−Буняковского:
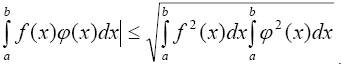
Дата добавления: 2015-01-24; просмотров: 738;