Основные свойства определенного интеграла
Свойство 1(о перестановке пределов)
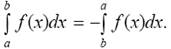
При введении определенного интеграла мы всегда подразумеваем, что a < b. Для случая a = b полагаем, по определению определенный интеграл равным нулю.
Свойство 2(о разбиении интервала интегрирования).
Каковы бы ни были числа a, b, c, имеет место равенство
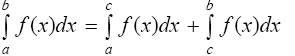
Здесь и в дальнейшем предполагается, что интегралы, входящие в формулы, существуют.
Из свойства 2 следует, что если с1, с2, …, сk – как угодно расположенные числа в интервале непрерывности функции f(x), то
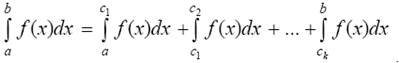
Свойство 2 называют свойством аддитивности определенного интеграла.
Свойство 3(линейности)
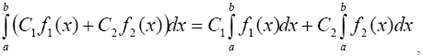
где С1, С2 − постоянные числа.
Замечание. Свойство 3 имеет место для любого числа слагаемых. Это свойство говорит о том, что постоянный множитель можно выносить за знак интеграла, а интеграл от суммы равен сумме интегралов.
Свойство 4(о знаке интеграла)
Если всюду на отрезке [a, b] функция f(x) ≥ 0 (f(x) ≤ 0), то
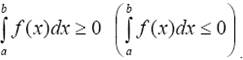
Свойство 5(об интегрировании неравенств)
Если всюду на отрезке [a, b] функция f(x) ≤ g(x), то
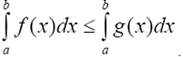
Дата добавления: 2015-01-24; просмотров: 1080;
