Первообразная и неопределенный интеграл.
Свойства неопределенного интеграла.
Таблица интегралов
При изучении дифференцирования функций, ставилась задача − по данной функции найти ее производную или дифференциал. Многие вопросы науки и техники приводят к постановке обратной задачи − для данной функции f(x) найти такую функцию F(x), производная или дифференциал которой равны соответственно f(x) или f(x)dx.
Определение 1.Функция F(x) называется первообразной по отношению к функции f(x) на некотором промежутке (a, b), если на этом промежутке функция F(x) дифференцируема и удовлетворяет уравнению
F ′(x) = f(x)
или, что то же самое, соотношению
dF(x) = f(x)dx.
Так, например, функция sin 5x – первообразная на любом промежутке по отношению к функции f (x) = 5cos5x, так как (sin5x)′ = 5cos5x .
Легко проверить, что наличие одной первообразной обеспечивает наличие таких функций в бесконечном множестве. В самом деле, если F(x) – первообразная от функции f(x), то
Ф(x) = F(x) + C,
где С – любая постоянная, также первообразная, так как
Ф ′(х) = (F(x) + C)′ = F ′(x) + 0 = f (x).
На вопрос, как найти все первообразные данной функции, если известна одна из них, дает ответ следующая теорема.
Теорема 1 (о первообразных). Если F(x) − какая-нибудь первообразная от функции f(x) на интервале (a, b), то все ее первообразные имеют вид F(x) + С, где С – произвольная постоянная.
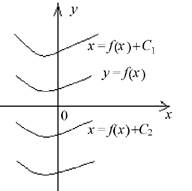
Геометрически y = F(x) + C означает, что график любой первообразной функции получается из графика функции y = F(x) простым сдвигом его параллельно оси Оу на величину С (см. рисунок). В связи с тем, что одна и та же функция f(x) имеет бесконечно много первообразных, возникает проблема выбора первообразной, которая решает ту или иную практическую задачу.
Известно, что производная от пути по времени равна скорости точки: S′(t) = V (t), поэтому, если известен закон изменения скорости V(t), путь движения точки есть первообразная от скорости точки, т. е. S(t) = F(t) + C.
Для нахождения закона изменения пути S(t) нужно использовать начальные условия, т. е. знать, чему равен пройденный путь S0 при t = t0. Пусть при t = t0 имеем S = S0. Тогда
S(t0 ) = S0 = F(t0 ) + C. С = S0 – F(t0 ) и S(t) = F(t) + S0 – F(t0 ).
Определение 2.Если F(x) – некоторая первообразная от функции f(x), то выражение F(x) + C, где С – произвольная постоянная, называется неопределенным интегралом и обозначается
∫f (x)dx = F(x) + C ,
т. е. неопределенный интеграл от функции f(x) есть множество всех её первообразных.
При этом функция f(x) называется подынтегральной,а произведение f(x)dx – подынтегральным выражением; F(x) – одна из первообразных; х – переменная интегрирования.Процесс отыскания первообразной называется
интегрированием.
П р и м е р 1. Найти неопределенные интегралы:
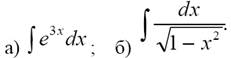
Решение

Теорема 2(существование неопределенного интеграла). Если функция f(х) непрерывна на (a, b) , то существует первообразная, а значит, и интеграл ∫f (x)dx.
Свойства неопределенных интегралов:
1. (∫f (x)dx)′= f (x) , т. е. производная от неопределенного интеграла равна подынтегральной функции.
2. d(∫f (x)dx)= f (x)dx , т. е. дифференциал от неопределенного интеграла равен подынтегральному выражению.
3. ∫dF(x) = F(x) + C .
4. ∫(C1 f1(x) +C2 f2 (x))dx = C1∫f1(x)dx + C2∫f2(x)dx − свойство линейности; С1, С2 – постоянные.
5. Если ∫f (x)dx = F(x) + C , то
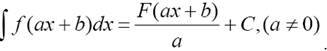
Первые три свойства вытекают из определения неопределенного интеграла. Свойств 4 и 5 получаем дифференцированием левых и правых частей уравнений по х, используя свойство 1 интегралов и свойства производных.
П р и м е р 2. Найти неопределенный интеграл: а) ∫(ex +cos5x)dx.
Решение. Используя свойства 4 и 5, находим:
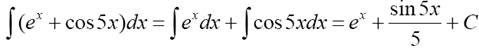
Приведем таблицу основных интегралов, которая в высшей математике играет такую же роль, как таблица умножения в арифметике.
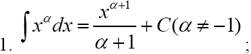

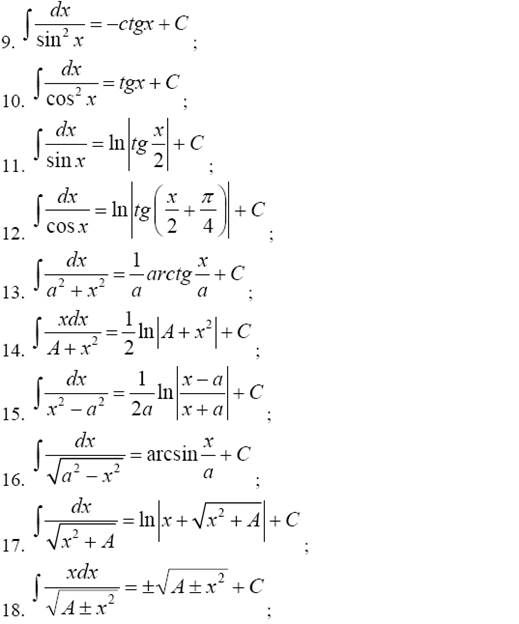
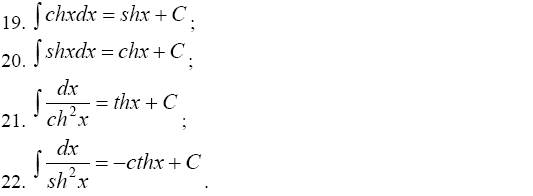
Дата добавления: 2015-01-24; просмотров: 3547;
