Основные методы интегрирования
Существует три основных метода интегрирования.
1. Непосредственное интегрирование − вычисление интегралов с помощью таблицы интегралов и основных свойств неопределенных интегралов.
П р и м е р 3. Вычислить интеграл: ∫tg 2 xdx.
Решение:
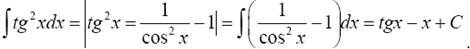
2. Метод подстановки. Во многих случаях введение новой переменной интегрирования позволяет свести вычисление данного интеграла к нахождению табличного. Этот метод еще называют методом замены переменной.
Теорема 3.Пусть функция x = φ(t) определена, непрерывна и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на нем, т. е. на Т определена сложная функция f(φ(t)). Тогда если ∫f(x)dx = F(x) +C , то
∫f(x)dx =∫f(φ(t)) φ ′(t)dt. (1)
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Замечание. После вычисления интеграла ∫f(φ(t)) φ ′(t)dt нужно перейти назад к переменной х.
П р и м е р 4. Найти интеграл: ∫cos3x sinxdx.
Решение:
а) Заменим sinxdx на (−d cos x), т. е. внесем функцию cos x под знак дифференциала. Получим
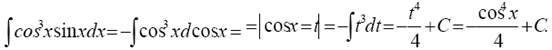
3. Метод интегрирования по частям
Теорема 4.Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть u′(x)v(x) имеет первообразную на этом промежутке, т. е. существует интеграл∫u′(x)v(x)dx. Тогда на этом промежутке имеет первообразную и функция u(x)v′(x) и справедлива формула
∫u(x)v′(x)dx = u(x)v(x) −∫v(x)u′(x)dx (2)
или
∫udv = uv −∫vdu . (2′)
Формулы (2) и (2′) называются формулами интегрирования по частям в неопределенном интеграле.
Методом интегрирования по частям вычисляются интегралы от следующих функций: P(x)arcsin(ax), P(x)arccos(ax), P(x)arctg(ax), P(x)arcctg(ax), P(x)ln x, P(x)ekx, P(x)sin kx, P(x)cos kx, здесь P(x) – многочлен; eax cosbx, eax sin bx.
Конечно, эти функции не исчерпывают всех интегралов, которые вычисляются с помощью метода интегрирования по частям.
П р и м е р 6. Найти интеграл: ∫arctg3xdx.
Решение. Положим u = arctg3x; dv = dx. Тогда
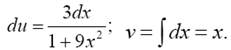
По формуле (2) имеем
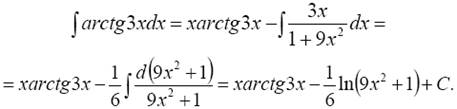
Дата добавления: 2015-01-24; просмотров: 1673;
