Касательные напряжения, полярный момент инерции сечения

Напомним, что связь напряжений и внутренних факторов в случае растяжения и сдвига была весьма простой:

, .

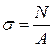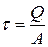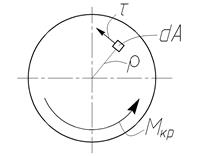
В кручении же требуется более детальное исследование. Действие касательных напряжений 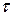должно в совокупности приводить к внутреннему крутящему моменту .

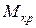Рассмотрим схему

, ,

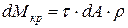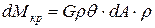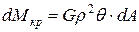
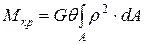(4.1)

Величины типа 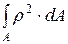весьма часто встречаются в ММ. Их изучение составляет отдельный раздел «Геометрия площадей». Величина 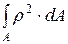в формуле 4.1. называется полярным моментом инерции сечения .

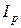Тогда получим

, ,

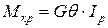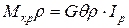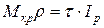
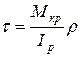(4.2)

Выражение 4.2 является искомой связью между напряжением и внутренним фактором при кручении. Получается, что чем больше площадка удалена от центра, тем больше касательные напряжения.

С другой стороны:

, , ,

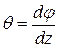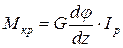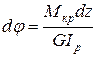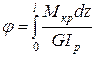(4.3)

Выражение 4.3 является формулой для определения полного угла закручивания.

Произведение 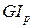в формуле 4.3 называется жесткостью при кручении.

Относительный угол закручивания из 4.1 будет

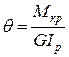
========================= 4 =========================