УРАВНЕНИЯ КОЛМОГОРОВА

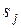При составлении системы дифференциальных уравнений (6) удобно пользоваться размеченным графом состояний системы, где возле каждой стрелки, ведущей из состояния в состояние , стоит интенсивность 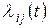пуассоновского потока событий, переводящего систему из состояния в 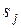. Если 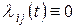ни стрелка, ни соответствующая интенсивность на размеченном графе не ставятся.

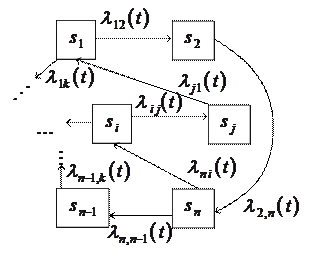Рис. 3

При составлении уравнений Колмогорова по графу состояний удобно ввести понятие «потока вероятности». Будем называть потоком вероятности, переводящим систему из состояния в состояние 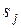произведение вероятности 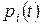состояния , из которого исходит стрелка, на интенсивность

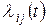потока событий переводящего систему по этой стрелке.

Уравнения Колмогорова (6) составляются по следующему правилу: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумма всех потоков вероятности выводящих систему из этого состояния.

Все интенсивности 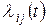в уравнении (6) можно записать в виде квадратной матрицы:

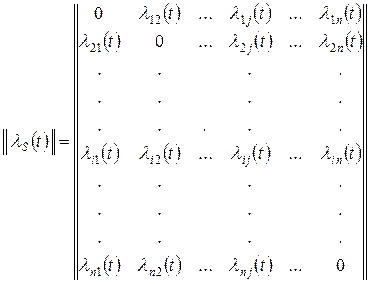, (17)

где 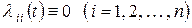. По главной диагонали этой матрицы размерности 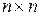стоят нули, а на пересечении i-й строки и j-го столбца стоит функция 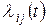- интенсивность пуассоновского потока событий, переводящих в систему S из состояния в состояние .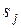

Матрицу интенсивностей (17) удобно иллюстрировать с помощью размеченного графа состояний системы S, на котором указываются только те ребра между состояниями и 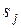для которых соответствующие интенсивности не равны нулю, а около каждого ребра проставляется соответствующая интенсивность потока событий (рис.5). Между матрицей интенсивностей (17) и размеченным графом состояний системы 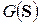существует однозначное соответствие.

Зная размеченный граф состояний системы 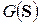(или матрицу интенсивностей 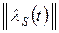), можно, воспользовавшись мнемоническим правилом, записать систему дифференциальных уравнений для вероятностей состояний системы (6).

Если все интенсивности потоков 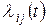не зависят от аргумента t 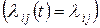, то марковский процесс называется однородным. Если хотя бы одна из интенсивностей в матрице (17) зависит от времени, то такой марковский процесс называется неоднородным. У однородного марковского процесса коэффициенты в системе дифференциальных уравнений (6) являются постоянными.

Таким образом, для исследования марковского случайного процесса нужно знать: 1) матрицу интенсивностей 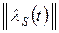(17) (или размеченный граф состояний системы 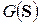) и 2) начальные условия

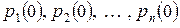, (18)

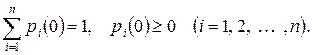(19)

Пример. Размеченный граф состояний системы имеет вид, показанный на рис. 4.

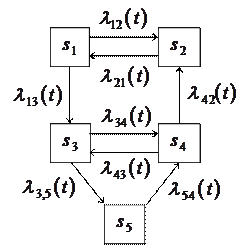Рис. 4

Написать уравнения Колмогорова для вероятностей состояний и указать, при каких начальных условиях их нужно решать, если в начальный момент времени система S с вероятностью ½ находится в состоянии 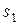и с вероятностью ½ - в состоянии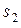

Решение. Уравнения Колмогорова имеют вид

(*)

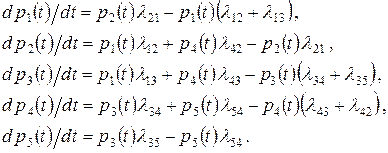Любое из этих уравнений может быть отброшено, а соответствующая ему вероятность 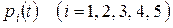выражена через остальные с помощью нормировочного условия:

. (**)

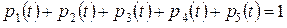Начальные условия, при которых надо будет решать систему дифференциальных уравнений, будут:

(***)

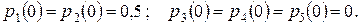Уравнения (*) как при постоянных, так и переменных интенсивностях 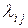(совместно с нормировочным условием (**)), можно решать на ЭВМ при начальных условиях (***) любым из перечисленных методов.