ВХОДЯЩИЙ ПОТОК ЗАЯВОК
Пусть теперь 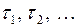 – моменты поступления заявок пуассоновского потока. Тогда для любого
– моменты поступления заявок пуассоновского потока. Тогда для любого 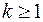 функция распределения
функция распределения
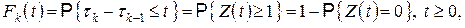
или 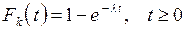 .
.
Таким образом, для пуассоновского входящего потока промежутки времени между моментами поступления заявок статистически независимы и имеют одинаковое экспоненциальное распределение.
Для пуассоновского входящего потока имеет место важное свойство отсутствия последействия: время ожидания поступления новой заявки не зависит от того, когда появилась предыдущая заявка. Поскольку интервалы между моментами поступления заявок имеют экспоненциальное распределение, точная формулировка этого свойства является следующей. Пусть случайная величина 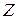 распределена по экспоненциальному закону, т.е.
распределена по экспоненциальному закону, т.е.
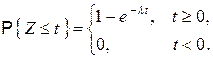
Тогда для любого числа 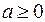
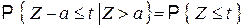 . (1)
. (1)
В общем случае входящий поток заявок определяется посредством задания для каждого 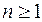 совместного распределения случайных величин
совместного распределения случайных величин 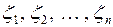 , где
, где 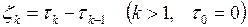 , а
, а 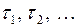 – моменты поступления заявок
– моменты поступления заявок 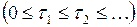 . В том случае, когда случайные величины
. В том случае, когда случайные величины 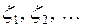 независимы в совокупности, для определения входящего потока достаточно задать набор одномерных функций распределения
независимы в совокупности, для определения входящего потока достаточно задать набор одномерных функций распределения 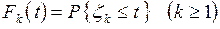 . Такой входящий поток называется потоком с ограниченным последействием. Естественным обобщением пуассоновского потока является поток, для которого
. Такой входящий поток называется потоком с ограниченным последействием. Естественным обобщением пуассоновского потока является поток, для которого 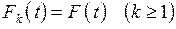 . Такой поток называется рекуррентным.
. Такой поток называется рекуррентным.
Рассмотрим ординарный поток однородных событий.

Этот поток называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательными событиями 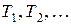 представляют собой независимые случайные величины.
представляют собой независимые случайные величины.
Очевидно, простейший поток является частным случаем потока Пальма: в нем расстояния 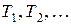 представляют собой независимые случайные величины, распределенные по показательному закону.
представляют собой независимые случайные величины, распределенные по показательному закону.
Рассмотрим примеры потоков Пальма.
1. Некоторая деталь технического устройства (например, радиолампа) работает непрерывно до своего отказа (выхода из строя), после чего она мгновенно заменяется новой. Срок безотказной работы детали случаен; отдельные экземпляры выходят из строя независимо друг от друга. При этих условиях поток отказов (или поток «восстановлений») представляет собой поток Пальма. Если, к тому же, срок работы детали распределен по показательному закону, то поток Пальма превращается в простейший.
2. Группа самолетов идет в боевом порядке «колонна» с одинаковой для всех самолетов скоростью 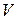 .
.

Каждый самолет, кроме ведущего, обязан выдерживать строй, т. е. держаться на заданном расстоянии 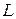 от впереди идущего. Это расстояние, вследствие погрешностей радиодальномера, выдерживается с ошибками. Моменты пересечения самолетами заданного рубежа образуют поток Пальма, так как случайные величины
от впереди идущего. Это расстояние, вследствие погрешностей радиодальномера, выдерживается с ошибками. Моменты пересечения самолетами заданного рубежа образуют поток Пальма, так как случайные величины 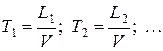 независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.
независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.
Интересным примером потоков с ограниченным последействием являются так называемые потоки Эрланга. Они образуются «просеиванием» простейшего потока.
Рассмотрим простейший поток и выбросим из него каждую вторую точку (на рисунке выброшенные точки отмечены крестами).

Оставшиеся точки образуют поток; этот поток называется потоком Эрланга первого порядка 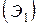 . Очевидно, этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то, независимы и величины
. Очевидно, этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то, независимы и величины 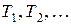 , получающиеся суммированием таких промежутков по два.
, получающиеся суммированием таких промежутков по два.
Поток Эрланга второго порядка получится, если сохранить в простейшем потоке каждую третью точку, а две промежуточные выбросить.

Вообще, потоком Эрланга k-го порядка 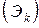 называется поток, получаемый из простейшего, если сохранить каждую
называется поток, получаемый из простейшего, если сохранить каждую 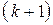 -ю точку, а остальные выбросить. Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка
-ю точку, а остальные выбросить. Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка 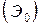 .
.
Дата добавления: 2015-01-19; просмотров: 1501;
