ПОКАЗАТЕЛИ КАЧЕСТВА СМО
Показатели качества. Математическая модель реальной системы строится так, чтобы оценить какие-то показатели качества этой системы. Для систем с очередями необходимо прежде всего оценить загруженность системы. Простейшей мерой загруженности является нагрузка 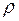 :
:
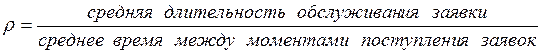 .
.
Если величины, стоящие в числителе и знаменателе этого отношения, равны соответственно 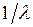 и
и 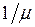 , то
, то 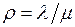 .
.
Если нагрузка превосходит единицу, то это означает, что заявки поступают быстрее, нежели их успевает обрабатывать обслуживающее устройство. В СМО с l параллельными обслуживающими устройствами на каждое из них приходится в среднем 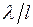 заявок в единицу времени. Поэтому нагрузка в такой СМО может быть поднята в l раз.
заявок в единицу времени. Поэтому нагрузка в такой СМО может быть поднята в l раз.
Процесс передачи заявок в системе с одним обслуживающим устройством проиллюстрирован на рисунке.
Диаграммы режимов работы СМО M/M/1. Установившийся режим

С нагрузкой тесно связан другой показатель качества – коэффициент использования, или коэффициент загрузки обслуживающего устройства. Этот показатель качества, обозначаемый через 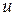 , определяется как доля времени, в течение которого обслуживающее устройство занято. Рассмотрим достаточно длительный интервал времени T. В СМО с l обслуживающими устройствами на каждое из них в среднем за время T придется по
, определяется как доля времени, в течение которого обслуживающее устройство занято. Рассмотрим достаточно длительный интервал времени T. В СМО с l обслуживающими устройствами на каждое из них в среднем за время T придется по 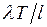 заявок в предположении, что поток заявок равномерно распределяется по l устройствам. Поскольку каждая заявка требует в среднем длительности обслуживания
заявок в предположении, что поток заявок равномерно распределяется по l устройствам. Поскольку каждая заявка требует в среднем длительности обслуживания 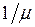 , то общее среднее время занятости обслуживающего устройства составит
, то общее среднее время занятости обслуживающего устройства составит 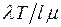 (сюда включены и простои обслуживающего устройства). Поделив эту величину на T, получим
(сюда включены и простои обслуживающего устройства). Поделив эту величину на T, получим 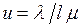 . Поскольку обслуживающее устройство не может быть занято более 100 % времени, то коэффициент использования не может превосходить единицу. Таким образом, получаем следующее выражение для коэффициента использования СМО с l обслуживающими устройствами:
. Поскольку обслуживающее устройство не может быть занято более 100 % времени, то коэффициент использования не может превосходить единицу. Таким образом, получаем следующее выражение для коэффициента использования СМО с l обслуживающими устройствами:
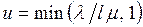 .
.
Для СМО с одним обслуживающим устройством коэффициент использования 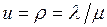 , если
, если 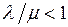 , т.е. совпадает с нагрузкой.
, т.е. совпадает с нагрузкой.
При анализе моделей вычислительных систем одним из основных показателей качества служит пропускная способность. Эта величина как среднее число заявок, обслуженных за единицу времени. В СМО с l обслуживающими устройствами за каждую единицу времени в среднем завершается обслуживание 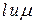 заявок, откуда вытекает, что пропускная способность равна
заявок, откуда вытекает, что пропускная способность равна
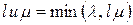 .
.
Таким образом, пропускная способность совпадает с интенсивностью поступления заявок 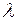 до тех пор, пока
до тех пор, пока 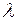 меньше максимальной интенсивности обслуживания
меньше максимальной интенсивности обслуживания 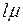 , выше которой пропускная способность не поднимается.
, выше которой пропускная способность не поднимается.
С точки зрения заявки самым важным показателем качества, по-видимому, является время, которое она проводит в ожидании обслуживания. Определим время ожидания 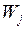 заявки j, равным отрезку времени от начала поступления заявки j в систему до начала ее обслуживания, а время ответа
заявки j, равным отрезку времени от начала поступления заявки j в систему до начала ее обслуживания, а время ответа 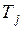 – равным отрезку времени от момента поступления заявки j в систему до момента завершения ее обслуживания. Таким образом, имеем следующее простое соотношение (индекс j опущен):
– равным отрезку времени от момента поступления заявки j в систему до момента завершения ее обслуживания. Таким образом, имеем следующее простое соотношение (индекс j опущен):
Время ответа (T) = время ожидания (W) + длительность обслуживания (S)
Для оценки качества СМО обычно применяются средние значения случайных величин 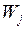 и
и 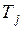 в установившемся (стационарном) режиме, когда
в установившемся (стационарном) режиме, когда 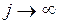 . Эти средние уже не зависят от j, и мы будем обозначать их символами
. Эти средние уже не зависят от j, и мы будем обозначать их символами 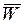 и
и 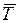 соответственно.
соответственно.
Более подробную информацию о качестве СМО могут дать функции распределения 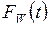 и
и 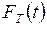 случайных величин
случайных величин 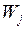 и
и 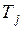 в установившемся режиме
в установившемся режиме 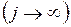 . Примером, где такие распределения представляют интерес, может служить случай, когда заявка может покинуть систему, если задержки велики.
. Примером, где такие распределения представляют интерес, может служить случай, когда заявка может покинуть систему, если задержки велики.
Последней интересующей нас мерой загруженности является длина очереди. Пусть случайный процесс 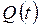 есть число заявок, ожидающих обслуживания в момент времени t. Аналогично, определим
есть число заявок, ожидающих обслуживания в момент времени t. Аналогично, определим 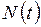 как число заявок, находящихся в системе – либо в очереди, либо на обслуживании. Процесс
как число заявок, находящихся в системе – либо в очереди, либо на обслуживании. Процесс 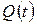 называют длиной очереди. В СМО с l обслуживающими устройствами
называют длиной очереди. В СМО с l обслуживающими устройствами 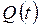 и
и 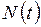 связаны соотношением
связаны соотношением
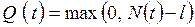 .
.
Изучение распределения числа заявок, ожидающих обслуживания, требуется, например, при оценке объема буферной памяти, необходимой для размещения поступающих заявок.
Процессы 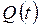 и
и 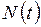 – это случайные процессы с непрерывным временем. Поэтому для оценки качества СМО, также как и в случае случайных последовательностей
– это случайные процессы с непрерывным временем. Поэтому для оценки качества СМО, также как и в случае случайных последовательностей 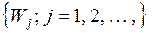 и
и 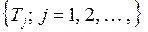 , применяются средние значения случайных процессов
, применяются средние значения случайных процессов 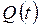 и
и 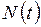 в установившемся режиме, когда
в установившемся режиме, когда 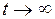 . Эти средние уже не зависят от t, и мы будем обозначать их символами
. Эти средние уже не зависят от t, и мы будем обозначать их символами 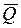 и
и 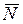 соответственно.
соответственно.
Выведем (без излишней строгости) некоторые важные соотношения для показателей качества СМО 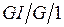 в установившемся режиме. Пусть заданы
в установившемся режиме. Пусть заданы 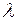 – интенсивность поступления заявок в СМО и
– интенсивность поступления заявок в СМО и 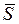 – средняя длительность обслуживания заявки. Интенсивность обслуживания заявок работающим устройством есть
– средняя длительность обслуживания заявки. Интенсивность обслуживания заявок работающим устройством есть 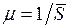 , а интенсивность выходящего потока заявок в произвольный момент времени равна
, а интенсивность выходящего потока заявок в произвольный момент времени равна 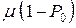 , где
, где 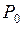 – вероятность простоя обслуживающего устройства в установившемся режиме, т.е.
– вероятность простоя обслуживающего устройства в установившемся режиме, т.е. 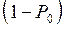 – вероятность того, что устройство работает. Поскольку в установившемся режиме интенсивность ухода обслуженных заявок из системы совпадает с интенсивностью поступления заявок в систему, то
– вероятность того, что устройство работает. Поскольку в установившемся режиме интенсивность ухода обслуженных заявок из системы совпадает с интенсивностью поступления заявок в систему, то 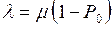 . Отсюда
. Отсюда
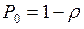 ,
,
где 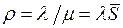 – нагрузка, или коэффициент использования обслуживающего устройства. Как следует из (5), в установившемся режиме
– нагрузка, или коэффициент использования обслуживающего устройства. Как следует из (5), в установившемся режиме 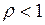 .
.
Дата добавления: 2015-01-19; просмотров: 1701;
