СОСТОЯНИЯМИ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ

Нам будет удобно считать, что переходы системы S из состояния в состояние происходят под воздействие каких-то потоков событий, например, «поток отказов», «поток восстановлений» и т. д.; как только произошло первое после момента 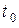событие, переход из состояния в состояние осуществляется (последующие события потока не учитываются никак).

Предполагаем, что переходы из состояния в состояние происходят под воздействием пуассоновских потоков событий (не обязательно стационарных).

Отсутствие последействия в пуассоновском потоке позволит нам при фиксированном настоящем (состояние системы в момент t) не заботиться о том, когда и как система оказалась в этом состоянии.

Пусть на графе состояний системы S существует стрелка, ведущая из состояния в одно из соседних состояний (рис. 1).

Рис 1. Рис. 2

Будем считать, что переход из состояния в состояние 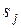осуществляется под воздействием пуассоновского потока с интенсивностью 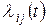. Переход из в 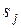происходит в момент, когда наступает первое событие потока.

Рассмотрим на оси 0t элементарный участок времени 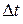, примыкающий к t (рис. 2), и найдем вероятность того, что за время 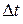система S перейдет из состояния в состояние 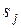(в предположении, что в момент времени t система S находилась в состоянии ). Эта вероятность, с точностью до бесконечно малых величин высших порядков равна 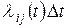. Действительно случайная величина 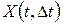, равная числу событий потока попадающих на элементарный участок 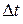, имеет математическое ожидание 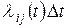, и с точностью до бесконечно малых высших порядков равна вероятности 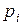попадания на элементарный участок одного (а значит хотя бы одного) события (вероятностью попадания на участок 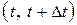более одного события пренебрегаем).

Итак, вероятность перехода системы S из состояния , в котором она находилась в момент времени t, в состояние 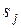за элементарный промежуток времени 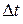, непосредственно примыкающий к t , приближенно равна 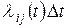, где 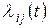– интенсивность пуассоновского потока событий переводящего систему из в .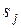

Можно доказать, что если известны все потоки событий, переводящие систему из состояния в состояние, – пуассоновские и независимые, то процесс протекающий в системе S, будет марковским.

Если известны все интенсивности пуассоновских потоков событий, переводящих систему из состояния в состояние, то можно составить дифференциальные уравнения для вероятностей состояний.

Рассмотрим систему S, имеющую n возможных состояний: 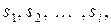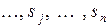. Пусть для любой пары состояний , 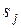известна интенсивность 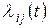пуассоновского потока событий переводящего систему S из любого состояния в любое другое состояние 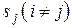; будем полагать эту интенсивность равной нулю, если непосредственный переход из состояния в состояние 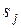невозможен. Обозначим 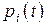– вероятность того, что в момент t система находится в состоянии 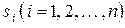. Теперь придадим t приращение 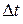и найдем вероятность 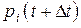того, что в момент 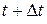система будет находиться в состоянии . Обозначим это событие A: .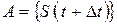

Зададим вопрос, как это событие может произойти? Двумя способами: либо произойдет событие B, состоящее в том, что в момент t система уже была в состоянии и за время 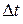не вышла из этого состояния; либо произойдет событие C , состоящее в том, что в момент t система была в одном из соседних состояний 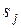, из которых возможен переход в 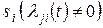и за время 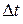перешла из состояния 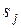в .

Очевидно 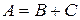. Найдем вероятности событий B и C. Согласно правилу умножения вероятностей вероятность события B вероятности 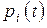того, что система в момент t была в состоянии , умноженную на условную вероятность того, что за время 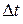она не выйдет из этого состояния, т. е. в суммарном потоке событий, выводящих систему из состояния , не появится ни одного события. Так как суммарный поток событий, выводящий систему из состояния , как и все его слагаемые – пуассоновский с интенсивностью, равной сумме интенсивностей слагаемых потоков:

,

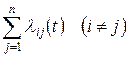то условная вероятность того, что на участке времени 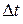появится хотя бы одно событие, равна (приближенно)

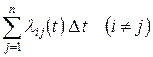[1],

а условная вероятность противоположного события равна 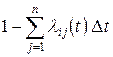. Таким образом,

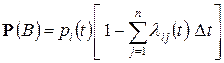. (1)

Найдем теперь вероятность события C. Представим его в виде суммы несовместных вариантов

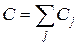, (2)

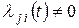где суммирование распространяется на все состояния , их которых возможен непосредственный переход в (т. е. для которых ). События 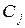, в силу ординарности потоков, можно считать несовместимыми. По правилу сложения вероятностей

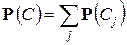. (3)

По правилу умножения вероятностей

,

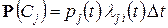откуда

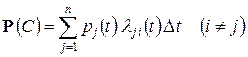, (4)

следовательно

.

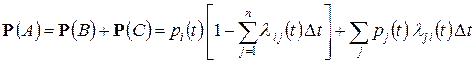Таким образом,

.

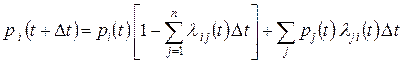Вычитая из (5) 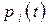, получим приращение функции на участке :

;

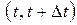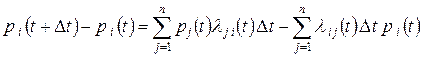деля приращение функции на приращение аргумента 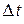и устремляя 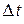к нулю, получим в пределе производную функции :

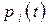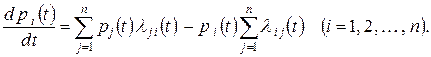(6)

Первая сумма в правой части формулы (6) распространяется на те значения j, для которых возможен непосредственный переход из состояния 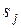в (т. е. для которых 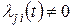), а вторая – на те значения j , для которых возможен непосредственный переход из в 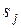(т. е. ).

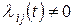Таким образом, мы получили для вероятностей 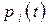систему обыкновенных дифференциальных уравнений (6) с переменными (в общем случае) коэффициентами. Эти уравнения называются уравнениями Колмогорова.

Систему дифференциальных уравнений (6) решают при начальных условиях, задающих вероятности состояний в начальный момент времени при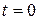

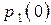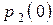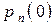, , … , , (7)

причем для любого момента времени t выполняется нормировочное условие

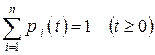. (8)

Это следует из того, что в любой момент времени t события

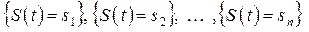
образуют полную группу несовместных событий. Нормировочное условие (8) можно использовать вместо одного (любого) из дифференциальных уравнений (6).