ПУАССОНОВСКИЙ ПРОЦЕСС
Пуассоновский процесс можно рассматривать с различных точек зрения, и здесь мы рассмотрим его в качестве прототипа всех процессов из этой главы. Последующий вывод распределения Пуассона наилучшим образом подходит для наших обобщений, однако он никоим образом не является лучшим и в других контекстах.
В качестве эмпирических предпосылок возьмем такие случайные события, как распад частиц, поступающие телефонные вызовы, расщепление хромосом под воздействием вредной радиации. Предполагается, что все наблюдаемые события однотипны, и мы интересуемся полным числом 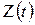 событий, происшедших в течение произвольного интервала времени длины
событий, происшедших в течение произвольного интервала времени длины 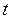 . Каждое событие представляется точкой на оси времени, и поэтому мы в действительности рассматриваем некоторые случайные размещения точек на прямой. Лежащие в основе нашей математической модели физические предположения состоят в том, что силы и воздействия, управляемые процессом, остаются постоянными, так, что вероятность любого отдельного события одна и та же для всех интервалов времени продолжительности
. Каждое событие представляется точкой на оси времени, и поэтому мы в действительности рассматриваем некоторые случайные размещения точек на прямой. Лежащие в основе нашей математической модели физические предположения состоят в том, что силы и воздействия, управляемые процессом, остаются постоянными, так, что вероятность любого отдельного события одна и та же для всех интервалов времени продолжительности 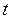 и не зависит от прошлого развития процесса. Математически это означает, что наш процесс является однородным по времени марковским процессом. Выведем основные вероятности
и не зависит от прошлого развития процесса. Математически это означает, что наш процесс является однородным по времени марковским процессом. Выведем основные вероятности
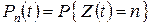 .
.
Чтобы ввести понятия, подходящие и для других процессов из этой главы, мы выберем начало отсчета времени и будем говорить, что в момент времени 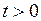 система находится в состоянии
система находится в состоянии 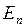 , если между 0 и
, если между 0 и 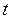 произошло ровно
произошло ровно 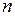 скачков функции
скачков функции 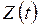 . Тогда
. Тогда 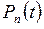 равняется вероятности состояния
равняется вероятности состояния 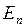 в момент
в момент 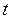 , однако
, однако 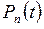 может быть также описана как вероятность перехода из произвольного состояния
может быть также описана как вероятность перехода из произвольного состояния 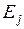 в произвольный момент времени
в произвольный момент времени 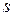 в состояние
в состояние 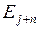 к моменту
к моменту 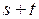 . Теперь наше нестрогое описание процесса мы преобразуем в свойства вероятностей
. Теперь наше нестрогое описание процесса мы преобразуем в свойства вероятностей 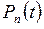 .
.
Здесь обязательно дать рисунки с точками на интервале [0, 1] с последовательным уменьшением h.
Разобьем временной интервал единичной длины на 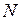 подинтервалов длины
подинтервалов длины 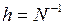 . Вероятность скачка внутри любого из этих подинтервалов равна
. Вероятность скачка внутри любого из этих подинтервалов равна 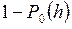 , и поэтому математическое ожидание числа интервалов, содержащих скачки, равно
, и поэтому математическое ожидание числа интервалов, содержащих скачки, равно 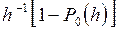 . Интуитивно представляется, что при
. Интуитивно представляется, что при 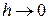 это число должно стремиться к математическому ожиданию числа скачков внутри произвольного интервала времени единичной длины, и поэтому естественно предположить, что существует число
это число должно стремиться к математическому ожиданию числа скачков внутри произвольного интервала времени единичной длины, и поэтому естественно предположить, что существует число 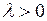 такое, что
такое, что
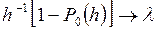 . (2)
. (2)
Физическая картина процесса требует также, чтобы скачок обязательно приводил из состояния 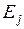 в соседнее состояние
в соседнее состояние 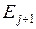 , и отсюда вытекает, что математическое ожидание числа подынтервалов (длины
, и отсюда вытекает, что математическое ожидание числа подынтервалов (длины 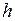 ), содержащих более чем один скачок, должно стремиться к 0. Поэтому мы должны предположить, что при
), содержащих более чем один скачок, должно стремиться к 0. Поэтому мы должны предположить, что при 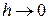
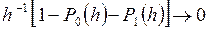 . (3)
. (3)
Чтобы окончательно сформулировать постулаты, запишем (2) в виде 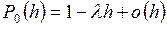 , где (как обычно)
, где (как обычно) 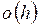 обозначает величину, по порядку меньшую чем
обозначает величину, по порядку меньшую чем 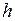 . (Точнее говоря,
. (Точнее говоря, 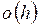 означает такую величину, что
означает такую величину, что 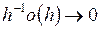 при
при 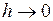 ). С учетом этого (3) эквивалентно соотношению
). С учетом этого (3) эквивалентно соотношению 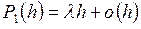 . Сформулируем теперь следующие постулаты.
. Сформулируем теперь следующие постулаты.
Постулаты пуассоновского процесса. Процесс начинается в момент времени 0 в состоянии 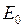 (
( 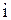 ). Непосредственный переход из состояния
). Непосредственный переход из состояния 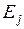 возможен только в состояние
возможен только в состояние 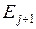 (
( 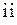 ). Каково бы ни было состояние
). Каково бы ни было состояние 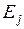 процесса в момент времени
процесса в момент времени 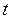 , (условная) вероятность скачка внутри последующего короткого интервала времени между
, (условная) вероятность скачка внутри последующего короткого интервала времени между 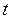 и
и 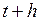 равна
равна 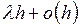 , тогда как (условная) вероятность наличия в нем более чем одного скачка есть
, тогда как (условная) вероятность наличия в нем более чем одного скачка есть 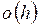 .
.
Наши постулаты носят чисто аналитический характер, и их достаточно, чтобы показать, что мы должны иметь
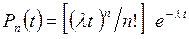 . (4)
. (4)
Для доказательства этого возьмем сперва 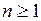 и рассмотрим событие, состоящее в том, что в момент времени
и рассмотрим событие, состоящее в том, что в момент времени 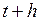 система находится в состоянии
система находится в состоянии 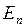 . Вероятность этого события равна
. Вероятность этого события равна 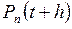 , и осуществиться оно может тремя взаимоисключающими способами.
, и осуществиться оно может тремя взаимоисключающими способами.
Во-первых, в момент времени 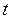 система может находиться в состоянии
система может находиться в состоянии 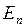 , и между
, и между 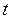 и
и 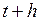 не произойдет ни одного скачка. Вероятность этой возможности равна
не произойдет ни одного скачка. Вероятность этой возможности равна
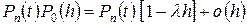 .
.
Вторая возможность состоит в том, что в момент времени 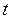 система находится в состоянии
система находится в состоянии 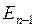 и между
и между 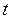 и
и 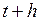 происходит в точности один скачок. Вероятность этого равна
происходит в точности один скачок. Вероятность этого равна
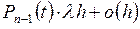 .
.
Любое другое состояние в момент 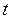 потребует более одного скачка в интервале между
потребует более одного скачка в интервале между 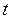 и
и 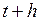 , и вероятность подобного события есть
, и вероятность подобного события есть 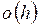 .
.
Следовательно, мы должны иметь
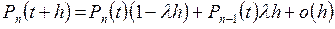 , (5)
, (5)
а это соотношение можно переписать в виде
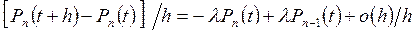 . (6)
. (6)
При 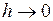 последний член стремится к нулю; следовательно, предел левой части существует и равен
последний член стремится к нулю; следовательно, предел левой части существует и равен
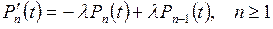 . (7)
. (7)
При 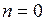 вторая и третья из упомянутых выше возможностей не возникают, и поэтому (5) следует заменить на
вторая и третья из упомянутых выше возможностей не возникают, и поэтому (5) следует заменить на
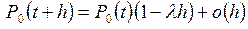 , (8)
, (8)
что приводит к
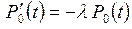 . (9)
. (9)
Отсюда и из 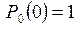 получаем
получаем 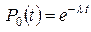 . Подставляя это значение
. Подставляя это значение 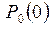 в (7) при
в (7) при 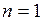 , мы получим обыкновенное дифференциальное уравнение для
, мы получим обыкновенное дифференциальное уравнение для 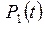 .
.
Легко проверить путем подстановки в формулу (7) и проверки тождества левой и правой частей, что 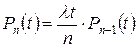 ,
, 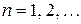 . Поскольку
. Поскольку 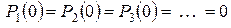 , мы легко находим, что
, мы легко находим, что
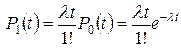 ,
,
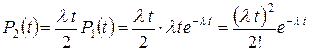 ,
,
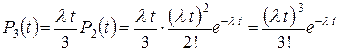 ,
,
… ,
а это полностью согласуется с (4).
Дата добавления: 2015-01-19; просмотров: 2042;
