ЗА НЕСКОЛЬКО ШАГОВ
Мы обозначим через 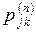 вероятность перехода из
вероятность перехода из 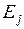 в
в 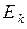 ровно за
ровно за 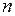 шагов. Иначе говоря
шагов. Иначе говоря 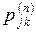 есть условная вероятность попадания в
есть условная вероятность попадания в 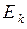 на
на 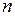 -м шаге при условии, что начальным состоянием. Было
-м шаге при условии, что начальным состоянием. Было 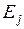 ; она равна сумме вероятностей всех путей
; она равна сумме вероятностей всех путей 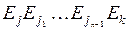 длины
длины 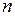 , начинающихся в
, начинающихся в 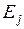 и оканчивающихся в
и оканчивающихся в 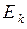 . В частности,
. В частности, 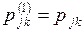 и
и
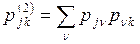 . (1)
. (1)
По индукции мы получаем общую рекуррентную формулу
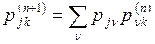 (2)
(2)
дальнейшая индукция по 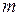 приводит к основному тождеству
приводит к основному тождеству
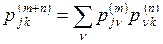 . (3)
. (3)
(которое является частным случаем уравнения Колмогорова-Чепмена). Оно отражает тот простой факт, что первые 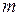 шагов приводят из
шагов приводят из 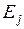 в некоторое промежуточное состояние
в некоторое промежуточное состояние 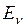 и что вероятность последующего перехода из
и что вероятность последующего перехода из 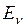 в
в 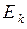 не зависит от того, каким образом было достигнуто
не зависит от того, каким образом было достигнуто 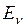 .
.
Так же как и в случае 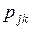 , образовавших матрицу
, образовавших матрицу 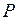 , мы расположим
, мы расположим 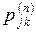 в матрицу, которую обозначим
в матрицу, которую обозначим 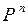 . Тогда (2) утверждает, что для того, чтобы получит элемент
. Тогда (2) утверждает, что для того, чтобы получит элемент 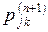 матрицы
матрицы 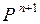 , мы должны умножить элементы
, мы должны умножить элементы 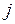 -й строки
-й строки 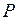 на соответствующие элементы
на соответствующие элементы 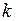 -го столбца
-го столбца 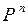 и сложить полученные произведения. Эта операция называется умножением матриц
и сложить полученные произведения. Эта операция называется умножением матриц 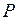 и
и 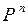 и выражается символически равенством
и выражается символически равенством 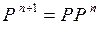 . Данное определение позволяет назвать
. Данное определение позволяет назвать 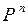
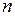 -й степенью
-й степенью 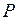 ; уравнение (3) выражает известный закон
; уравнение (3) выражает известный закон 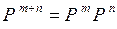 .
.
Для того чтобы (3.3) было справедливо для всех 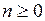 , мы определим
, мы определим 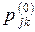 , положив
, положив 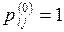 и
и 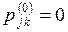 при
при 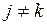 , что вполне естественно.
, что вполне естественно.
Пример. Независимые испытания. Обычно бывает трудно получить явные выражения для вероятностей перехода за несколько шагов, однако, к счастью они не представляют особого интереса. Как важное, хотя и тривиальное исключение, мы отметим частный случай независимых испытаний. Этот случай имеет место тогда, когда все строки 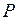 тождественно совпадают с данным распределением вероятностей, и ясно без вычислений, чт о отсюда следует равенство
тождественно совпадают с данным распределением вероятностей, и ясно без вычислений, чт о отсюда следует равенство 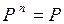 при всех
при всех 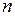 .
.
Безусловные вероятности
Пусть снова 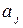 означает вероятность состояния
означает вероятность состояния 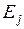 в начальном (нулевом) испытании. Тогда (безусловная) вероятность попадания в
в начальном (нулевом) испытании. Тогда (безусловная) вероятность попадания в 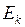 на
на 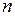 -м шаге равна
-м шаге равна
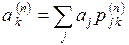 . (4)
. (4)
Обычно мы считаем, что процесс начинается из фиксированного состояния 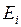 , т.е. полагаем
, т.е. полагаем 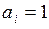 . В этом случае
. В этом случае 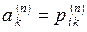 . Интуитивно мы чувствуем, что влияние начального состояния должно постепенно ослабевать, так как при больших
. Интуитивно мы чувствуем, что влияние начального состояния должно постепенно ослабевать, так как при больших 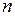 распределение (3.4) должно быть почти независимым от начального распределения
распределение (3.4) должно быть почти независимым от начального распределения 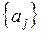 . Так оно и будет, если (как в последнем примере)
. Так оно и будет, если (как в последнем примере) 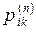 сходится к независящему от
сходится к независящему от 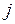 пределу, т.е. если
пределу, т.е. если 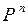 сходится к матрице с одинаковыми строками. Мы видим, что обычно это действительно так, хотя нам и придется еще принимать в расчет досадные исключения, обусловленные периодичностью.
сходится к матрице с одинаковыми строками. Мы видим, что обычно это действительно так, хотя нам и придется еще принимать в расчет досадные исключения, обусловленные периодичностью.
Пример. Вероятности перехода за несколько шагов
Вероятности перехода за несколько шагов проиллюстрируем сначала путем возведения матрицы в степень, оперируя стохастической матрицей.
Для определения всевозможных путей достижения нужного состояния (нужной вершины в графе) проделаем подобное возведение матрицы в степень с элементами, являющимися мнемоническими обозначениями путей.
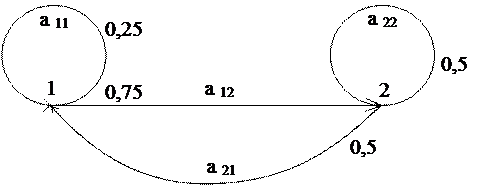
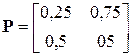 ; (за один шаг)
; (за один шаг)
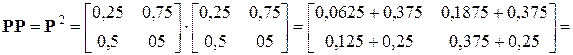
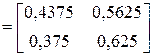 . (за 2 шага)
. (за 2 шага)
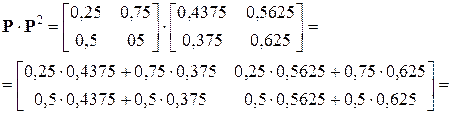
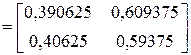 . (за 3 шага)
. (за 3 шага)
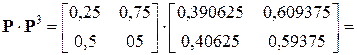
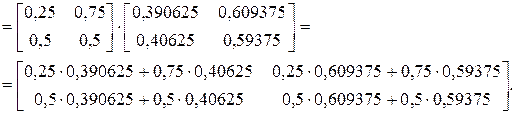
= 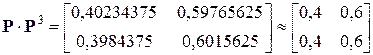 . (за 4 шага)
. (за 4 шага)
То же, но с символьными обозначениями для отслеживания путей
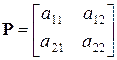 , (за один шаг)
, (за один шаг)
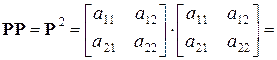 .
.
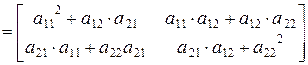 . (за 2 шага)
. (за 2 шага)
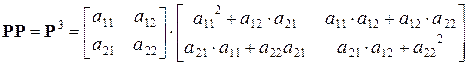 =
=
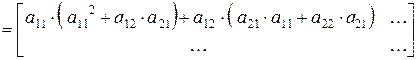 =
=
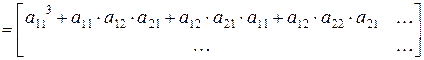 .
.
(за 3 шага из состояния 1 в то же состояние 1)
Дата добавления: 2015-01-19; просмотров: 1479;
