СВЕДЕНИЯ О ПРЕОБРАЗОВАНИИ ЛАПЛАСА-СТИЛТЬЕСА

Пусть 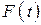– функция распределения случайной величины. Тогда

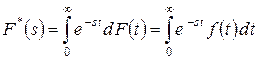
есть преобразование Лапласа-Стилтьеса этой функции. Например, если функция распределения характеризует экспоненциальную случайную величину 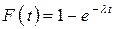, то легко получить .

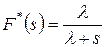Следует отличать преобразование Лапласа-Стилтьеса от обычного преобразования Лапласа 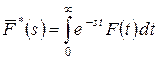. Связь между этими преобразованиями легко получить путем выполнения интегрирования по частям:

.

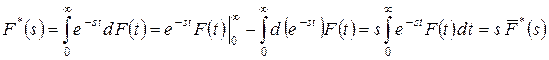Тогда для экспоненциального распределения

.

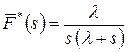Обратим внимание на некоторые важные свойства преобразования.

1. Важным свойством преобразования Лапласа-Стилтьеса является то, что преобразование Лапласа-Стилтьеса суммы случайных величин равно произведению преобразований Лапласа-Стилтьеса каждой из этих величин.

2. Если 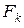есть k-й момент случайной величины относительно начала координат, то

,

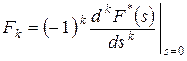т. е. моменты случайной величины определяются дифференцированием в нуле (при 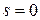) соответствующее число раз преобразования Лапласа-Стилтьеса функции распределения этой величины. Первый центральный момент определяет математическое ожидание (среднее значение) случайной величины,

,

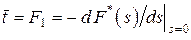а второй момент нужен для нахождения дисперсии случайной величины

.

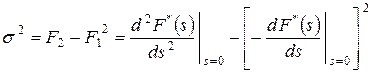3. Вероятностный смысл преобразования Лапласа-Стилтьеса. Величина 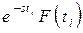есть вероятность сложного события, состоящего в том, что случайная величина не превысит значения 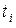(сомножитель 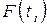), а кроме того, за время 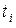не произойдет ни одной “катастрофы” (сомножитель 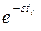). Параметр 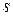рассматривается как интенсивность “катастроф”. Интегрирование по всему диапазону дает 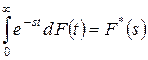. Таким образом, вероятностный смысл преобразования Лапласа-Стилтьеса состоит в том, что оно определяет вероятность того, что за время 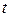не произойдет ни одной «катастрофы».

Распределение Пуассона задает число «катастроф» на отрезке 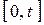в соответствии с формулой 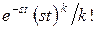, где s – интенсивность «катастроф», k – число «катастроф» на отрезке 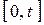. Если 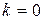, то катастроф не было, а вероятность этого равна 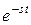. Более подробное изложение сведений о распределении Пуассона – в разделе, посвященном случайным процессам.