СВЕДЕНИЯ О НАЧАЛЬНЫХ МОМЕНТАХ СЛУЧАЙНЫХ ВЕЛИЧИН

В теории вероятностей наибольшую роль играет математическое ожидание, которое иногда называют просто средним значением случайной величины.

Подойдем к понятию математического ожидания, исходя из механической интерпретации распределения дискретной с. в. Пусть единичная масса распределена между точками оси абсцисс 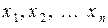, причем материальная точка 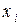имеет массу .

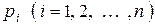Нам требуется выбрать на оси абсцисс точку, характеризующую положение всей системы материальных точек, с учетом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Обозначим абсциссу центра массы 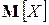. Имеем

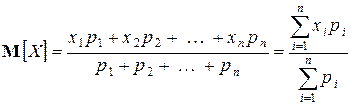
или, учитывая, что ,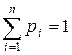

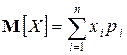. (1)

Это есть среднее взвешенное значение с. в. X , в которое абсцисса каждой точки 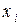входит с «весом», равным соответствующей вероятности.

Полученное таким образом среднее значение случайной величины X называется ее математическим ожиданием. Это – одно из важнейших понятий теории вероятностей. Дадим ему словесную формулировку.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.

Теперь рассмотрим случай, когда число возможных значений дискретной с. в. X не конечно, а бесконечно (образует счетное множество). Формула для математического ожидания остается такой же, только в верхнем пределе суммы n заменяется на бесконечность:

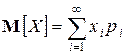. (2)

Некоторая сложность заключается в том, что бесконечная сумма (2) может и расходиться, т. е. соответствующая с. в. X – не иметь математического ожидания. Например, для X с рядом распределения

X:				…		…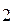
			…		…

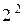
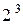
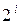
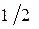
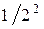
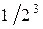
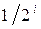
расходится (сумма его равна ∞), и, значит, у такой с. в. математического ожидания не существует.

Перейдем от дискретной с.в. X к непрерывной с плотностью 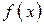. Механическая интерпретация математического ожидания сохранит тот же смысл: центр массы для единичной массы, распределенной непрерывно на оси абсцисс с плотностью 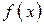. Заменяя в формуле (2) «скачущий» аргумент 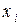непрерывно меняющимся x, а вероятность 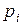– элементом вероятности 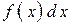, получим,

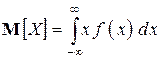. (3)

Разумеется, те значения x, для которых 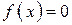, можно выбросить из области интегрирования. Так же, как и сумма (2), интеграл (3) может расходиться, и математическое ожидание – не существовать, но на практике обычно область значений с. в., для которых 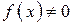, ограничена и математическое ожидание существует.

Математическое ожидание с. в. связано тесной зависимостью со среднеарифметическим ее наблюденных значений при большом числе опытов. Действительно, пусть имеется дискретная с. в. X с рядом распределения и k значениями:

X:			…		…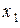
		…		…

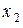
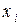
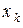
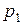
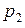
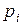
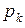
где 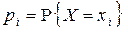. Пусть производится n независимых опытов, в каждом из которых с. в. X принимает определенное значение из множества 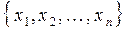. Предположим, что значение 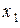появилось 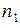раз, значение 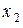– 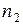раз и т. д.; 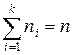. Среднее арифметическое наблюденных значений с. в. X обозначим 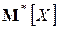. Имеем

.

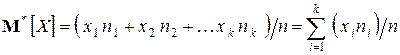Но 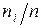есть не что иное, как частота (или статистическая вероятность) события 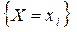; обозначим ее :

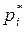итак,

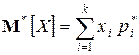, (4)

т. е. среднее арифметическое наблюденных значений с. в. равно сумме произведений ее возможных значений на соответствующие им частоты.

Мы знаем, что при увеличении числа опытов n частота события 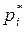будет приближаться (сходиться по вероятности) к вероятности 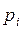этого события. Значит, и среднее арифметическое 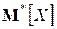будет приближаться (сходиться по вероятности) к математическому ожиданию 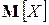случайной величины X. Это значит, что при достаточно большом числе опытов можно среднее арифметическое наблюденных значений с. в. X принимать приближенно равным ее математическому ожиданию.

Моменты, дисперсия, среднеквадратическое отклонение

Начальным моментом s-го порядка случайной величины X называется математическое ожидание s-той степени этой величины:

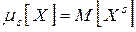. (1)

Для дискретной случайной величины X начальный момент s-го порядка выражается суммой:

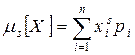(2)

где 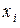– значения с. в. X, 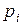– соответствующие вероятности; для непрерывной – интегралом:

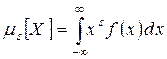, (3)

где 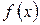– плотность распределения.

Ранее введенная характеристика положения – математическое ожидание с. в. – есть не что иное, как ее первый начальный момент

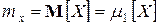. (4)

Дисперсия выражается через второй начальный момент

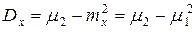
Или в других обозначениях:

,

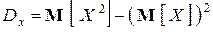т. е. дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат математического ожидания. Эту формулировку полезно запомнить.

Дисперсия случайной величины есть характеристика рассеивания, разбросанности с. в. около ее математического ожидания. Само слово «дисперсия» означает рассеивание.

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно; для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью с. в. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе «стандартом» или «стандартным отклонением») случайной величины. Будем обозначать его 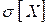(или )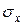

.

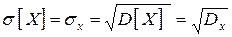Корень берется его арифметическим, т. е. положительным значением.

Для упрощения записей мы часто будем пользоваться сокращением 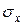для среднеквадратического отклонения (или просто 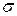, если ясно, о какой с. в. идет речь).

Для неотрицательной случайной величины X в качестве характеристики «степени ее случайности» иногда применяется коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию:

.

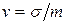Зная м. о. и с. к. о. случайной величины X , можно составить себе приближенное представление о диапазоне ее возможных значений. А именно, значения случайной величины X только изредка выходят за пределы интервала

,

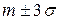и в большинстве случаев можно считать, что они укладываются в этот интервал. Это правило носит название «правила трех сигм». Согласно этому правилу для того, чтобы приближенно представить себе размах случайных отклонений с. в. X от ее м. о., достаточно отложить от точки m вправо и влево по отрезку, равному .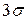

Дать неравенство Чебышева!

Неравенство Высочанского - Петунина. Единственным ограничением на функцию плотности распределения вероятности является то, что она должна быть одномодальной и иметь конечную дисперсию. Это неравенство справедливо, в том числе, и для резко асимметричных распределений, тем самым устанавливая границы для множества значений случайной величины, попадающих в определенный интервал.

Пусть X случайная величина с одномодальным распределением, средним значением μ и конечной ненулевой дисперсией 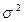. Тогда для любого

, .

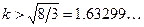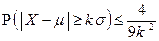В приложениях математической статистики очень часто используется эвристическое правило, при котором 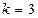, что соответствует верхней границе вероятности 4/81= 0,04938…, и таким образом строится граница, которая включает 95,06% значения случайной величины. В случае нормального распределения оценка улучшается до 99,73%.