ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКИМ МОДЕЛЯМ

Основными требованиями к математическим моделям являются требования адекватности, точности, экономичности.

Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность имеет место, если модель отражает заданные свойства объекта с приемлемой точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели.

Адекватность оценивается перечнем отражаемых свойств и областями адекватности. Область адекватности – область в пространстве параметров, в пределах которой погрешности модели остаются в допустимых пределах.

Пусть 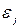относительная погрешность модели по 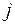-му выходному параметру:

,

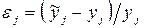где 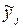– 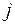-й выходной параметр, рассчитанный с помощью модели; 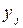– тот же параметр, имеющий место в моделируемом объекте.

Погрешность модели 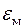по совокупности учитываемых выходных параметров оценивается одной из норм вектора 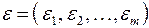, например

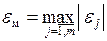или .

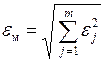Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельно допустимой погрешностью 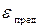, то можно в пространстве внешних параметров выделить область, в которой выполняется условие

.

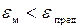Эту область называют областью адекватности (ОА) модели. Возможно введение индивидуальных предельных значений 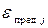для каждого выходного параметра и определение ОА как области, в которой одновременно выполняются все 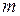условий вида .

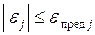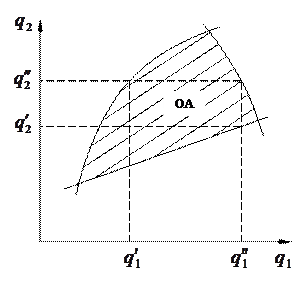Пример ОА (заштрихована) в двумерном пространстве дан на рисунке. Здесь 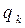– 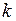-й внешний параметр.

Определение областей адекватности для конкретных моделей - сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства параметров. Определение ОА – более трудная задача, чем, например, задача параметрической оптимизации, поэтому для моделей вновь проектируемых объектов ОА не рассчитывают.

Однако для моделей унифицированных элементов расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании различных систем. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.

В общем случае ОА может иметь произвольную форму, сведения о которой выражаются громоздко, и неудобна в использовании, поэтому на практике вместо истинных ОА применяют те или иные их аппроксимации. Наиболее просто представляются и используются сведения об областях, имеющих форму гиперпараллелепипеда, который задается 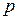двусторонними неравенствами:

,

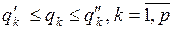где 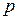- размерность пространства внешних параметров.

Так для одной из возможных макромоделей логического элемента транзисторно-транзисторной логики, реализующего функцию И-НЕ, рассчитанная область адекватности выражается следующими неравенствами:

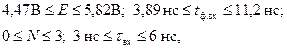
где 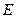– напряжения питания; 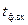– длительность фронта входного сигнала; 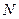- коэффициент нагружения; 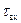– длительность входного сигнала.

В библиотеку моделей элементов наряду с алгоритмом, реализующим модель, и номинальными значениями параметров должны включаться граничные значения внешних параметров 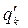и 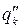, задающие область адекватности.

На рисунке дано графическое представление области адекватности и аппроксимирующего ее гиперпараллелепипеда. Такое представление удобно для двумерных случаев.

Возможно использование и других аппроксимаций ОА, например областей с линеаризованными границами в виде гиперплоскостей, областей в форме гиперсфер и т.п.

Экономичность (вычислительная эффективность) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, далее речь пойдет о характеристиках именно математических моделей, и экономичность будет характеризоваться затратами машинных времени и памяти.

Аналогичные требования по точности и экономичности фигурируют при выборе численных методов решения уравнений модели.