МОДЕЛИ И ИХ ПАРАМЕТРЫ
 цен
цен
Рис. 7.2 Структура показателя ROI
Представленную модель можно расширить, учитывая, что в показатель: материальные затраты, входят затраты на сырье, топливо, энергию, полуфабрикаты и т.п.; а затраты на оплату труда могут быть разложены на следующие составляющие: затраты на оплату труда рабочих и затраты на оплату труда служащих и т.д.
Аддитивные модели дают возможность проанализировать влияние явных факторов на относительный показатель, для управления неявными факторами используют мультипликативные модели, которые строят по следующим правилам:
· каждый фактор-сомножитель модели должен иметь самостоятельное экономическое значение;
· каждая пара прилегающих друг к другу факторов при перемножении должна давать новый показатель, имеющий самостоятельное значение;
· при перемножении всех факторов-сомножителей должен получаться исходный исследуемый показатель.
Примером мультипликативной модели эффективности производства может выступить модель, построенная на базе показателя, представляющего собой отношение материальных затрат к выручке от реализации. В качестве неявных факторов использованы следующие:
- зарплата;
- премиальный фонд;
- премии за экономию ресурсов;
- изменение стоимости активной части основных фондов;
- текучесть кадров;
- изменение доли рабочих в общей списочной численности работников;
- изменение доли активной части основных фондов.
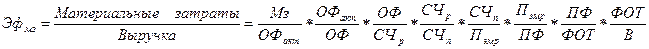
где ОФакт – стоимость активной части основных фондов;
Оф – стоимость основных фондов;
СЧр – списочная численность рабочих предприятия;
СЧп – списочная численность работников предприятия;
Пэмр – премии за экономию материальных ресурсов;
ПФ – общий премиальный фонд;
ФОТ – фонд оплаты труда.
Мультипликативная модель анализируется в динамике, поэтому рассчитывается индекс показателя:
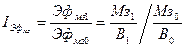 .
.
Необходимо отметить, что подробный и глубокий анализ отклонения показателя не всегда целесообразен, так требует достаточно много времени. Поэтому если причины отклонений очевидны, необходимость в детальном исследовании отпадает. Напротив, незначительное и непонятное на первый взгляд отклонение может заслуживать тщательного исследования, так как в результате могут быть выявлены признаки и тенденции, которые в будущем могут привести к возникновению проблем.
Контрольные вопросы
1. Каковы цели и задачи оперативного контроллинга?
2. Что представляет собой процесс бюджетирования и какие бюджеты используются предприятием в процессе управления деятельностью?
3. В чем заключается факторный и маржинальный методы анализа прибыли?
4. Для решения каких вопросов используется метод расчета точки безубыточности?
5. Назовите методы расчета сумм покрытия?
6. Какова структура показателя: рентабельность инвестиционного капитала.
7. В чем смысл использования аддитивных и мультипликативных моделей эффективности производства?
МОДЕЛИ И ИХ ПАРАМЕТРЫ
В автоматизированных проектных процедурах вместо еще не существующего проектируемого объекта оперируют некоторым квазиобъектом – моделью, которая отражает некоторые интересующие исследователя свойства объекта. Модель может быть физическим объектом (макет, стенд) или спецификацией. Среди моделей-спецификаций различают функциональные, поведенческие, информационные, структурные модели (описания). Эти модели называют математическими моделями, если они формализованы средствами аппарата и языка математики.
В свою очередь, математические модели могут быть геометрическими, топологическими, динамическими, логическими и т.п., если они отражают соответствующие свойства объектов. Наряду с математическими моделями при проектировании используют функциональные модели, информационные модели в виде диаграмм сущность-отношение, геометрические модели (чертежи). В дальнейшем, если нет специальной оговорки, под словом "модель" будем подразумевать математическую модель.
Математическая функциональная модель в общем случае представляет собой алгоритм вычисления вектора выходных параметров 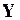 при заданных векторах параметров элементов (внутренних параметров)
при заданных векторах параметров элементов (внутренних параметров) 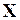 и внешних параметров
и внешних параметров 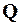 .
.
Математические модели могут быть символическими и численными. При использовании символических моделей оперируют не значениями величин, а их символическими обозначениями (идентификаторами). Численные модели могут быть аналитическими моделями, т.е. их можно представить в виде явно выраженных зависимостей выходных параметров 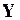 от параметров внутренних
от параметров внутренних 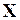 и внешних
и внешних 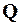 , или алгоритмическими моделями, в которых связь
, или алгоритмическими моделями, в которых связь 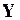 ,
, 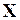 и
и 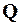 задана неявно в виде алгоритма моделирования. Важнейший частный случай алгоритмических моделей – имитационные модели, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель – это алгоритмическая поведенческая модель.
задана неявно в виде алгоритма моделирования. Важнейший частный случай алгоритмических моделей – имитационные модели, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель – это алгоритмическая поведенческая модель.
Классификацию математических моделей выполняют также по ряду других признаков.
Так, в зависимости от принадлежности к тому или иному иерархическому уровню выделяют модели уровней системного, функционально-логического, макроуровня (сосредоточенного) и микроуровня (распределенного).
По характеру используемого для описания математического аппарата различают модели лингвистические, теоретико-множественные, абстрактно-алгебраические, нечеткие, автоматные и т.п.
Например, на системном уровне преимущественно применяют модели систем массового обслуживания и сети Петри, на функционально-логическом уровне – автоматные модели на основе аппарата передаточных функций или конечных автоматов, на макроуровне – системы алгебро-дифференциальных уравнений, на микроуровне – дифференциальные уравнения в частных производных. Особое место занимают геометрические модели, используемые в системах конструирования.
Кроме того, введены понятия полных моделей и макромоделей, моделей статических и динамических, детерминированных и стохастических, аналоговых и дискретных, символических и численных.
Полная модель объекта в отличие от макромодели описывает не только процессы на внешних выводах моделируемого объекта, но и внутренние для объекта процессы.
Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т.е. в них обязательно используется время.
Стохастические и детерминированные модели различаются в зависимости от учета или неучета случайных факторов.
Информационные модели относятся к информационной страте автоматизированных систем, их используют прежде всего при инфологическом проектировании баз данных (БД) для описания связей между единицами информации.
Наибольшие трудности возникают при создании моделей слабоструктурированных систем, что характерно прежде всего для системного уровня проектирования. Здесь значительное внимание уделяется экспертным методам. В теории систем сформулированы общие рекомендации по подбору экспертов при разработке модели, организации экспертизы, по обработке полученных результатов. Достаточно общий подход к построению моделей сложных слабоструктурированных систем выражен в методиках IDEF.
Обычно в имитационных моделях фигурируют величины, характеризующие состояние моделируемой системы и называемые фазовыми переменными. Так, на макроуровне имитационные модели представляют собой системы алгебро-дифференциальных уравнений
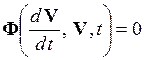 при
при 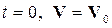 , (1)
, (1)
где 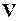 – вектор фазовых переменных;
– вектор фазовых переменных; 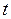 – время;
– время; 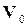 – вектор начальных условий. К фазовым переменным можно отнести токи и напряжения в электрических системах, силы и скорости – в механических, давления и расходы – в гидравлических.
– вектор начальных условий. К фазовым переменным можно отнести токи и напряжения в электрических системах, силы и скорости – в механических, давления и расходы – в гидравлических.
В аналоговых моделях фазовые переменные – непрерывные величины, в дискретных моделях – дискретные, в частном случае дискретные модели являются логическими (булевыми), в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев полезно применение смешанных моделей, в которых одна часть подсистем характеризуется аналоговыми моделями, другая – логическими.
Выходные параметры систем могут быть двух типов. Во-первых, это параметры-функционалы, т.е. функционалы зависимостей 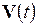 в случае использования (1). Примеры таких параметров: амплитуды сигналов, временные задержки, мощности рассеивания и т.п. Во-вторых, это параметры, характеризующие способность проектируемого объекта работать при определенных внешних условиях. Эти выходные параметры являются граничными значениями диапазонов внешних переменных, в которых сохраняется работоспособность объекта.
в случае использования (1). Примеры таких параметров: амплитуды сигналов, временные задержки, мощности рассеивания и т.п. Во-вторых, это параметры, характеризующие способность проектируемого объекта работать при определенных внешних условиях. Эти выходные параметры являются граничными значениями диапазонов внешних переменных, в которых сохраняется работоспособность объекта.
Дата добавления: 2015-01-19; просмотров: 1174;
