ЦЕПИ МАРКОВА. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Рассмотрим независимые испытания, которые можно описать следующим образом. Задано множество возможных исходов 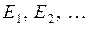 (в конечном или бесконечном числе), и каждому из них соотнесена некоторая вероятность
(в конечном или бесконечном числе), и каждому из них соотнесена некоторая вероятность 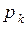 ; вероятности последовательностей исходов определяются по правилу умножения:
; вероятности последовательностей исходов определяются по правилу умножения: 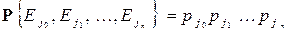 . В теории цепей Маркова мы рассматриваем простейшее обобщение этой схемы, которое состоит в том, что для любого испытания допускается зависимость его от непосредственно предшествующего ему испытания (и только от него). С исходом
. В теории цепей Маркова мы рассматриваем простейшее обобщение этой схемы, которое состоит в том, что для любого испытания допускается зависимость его от непосредственно предшествующего ему испытания (и только от него). С исходом 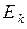 не связана более фиксированная вероятность
не связана более фиксированная вероятность 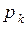 , но зато каждой паре
, но зато каждой паре 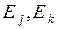 теперь соответствует условная вероятность
теперь соответствует условная вероятность 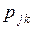 ; при условии, что
; при условии, что 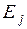 появился в некотором испытании, вероятность появления
появился в некотором испытании, вероятность появления 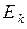 в следующем испытании равна
в следующем испытании равна 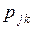 . Помимо
. Помимо 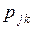 нам должны быть заданы вероятности
нам должны быть заданы вероятности 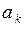 исходов
исходов 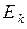 в начальном испытании. Чтобы
в начальном испытании. Чтобы 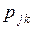 имели приписанный им смысл, вероятности последовательностей исходов, соответствующих двум, трем или четырем испытаниям, должны быть определены равенствами
имели приписанный им смысл, вероятности последовательностей исходов, соответствующих двум, трем или четырем испытаниям, должны быть определены равенствами
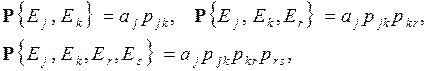
и вообще
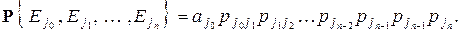 (1)
(1)
Здесь начальному испытанию присвоен номер нуль, так, что испытание номер один является вторым.
Определение. Последовательность испытаний с возможными исходами 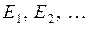 называется цепью Маркова, если вероятности последовательностей исходов определяются формулой (1) через распределение вероятностей
называется цепью Маркова, если вероятности последовательностей исходов определяются формулой (1) через распределение вероятностей 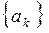 для
для 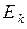 в начальном (или нулевом) испытании и через фиксированные условные вероятности
в начальном (или нулевом) испытании и через фиксированные условные вероятности 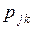 появления
появления 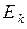 при условии, что в предыдущем испытании появился
при условии, что в предыдущем испытании появился 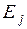 .
.
Для приложений цепей Маркова удобнее несколько видоизмененная технология. Возможные исходы 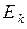 обычно называются возможными состояниями системы; вместо того, чтобы говорить, что
обычно называются возможными состояниями системы; вместо того, чтобы говорить, что 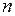 -е испытание окончилось появлением
-е испытание окончилось появлением 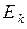 , говорят, что
, говорят, что 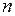 -й шаг приводит к состоянию
-й шаг приводит к состоянию 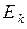 или что система попадает в
или что система попадает в 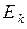 на
на 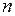 -м шаге. Наконец,
-м шаге. Наконец, 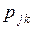 называется вероятностью перехода из
называется вероятностью перехода из 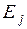 в
в 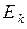 . Как обычно, мы считаем, что испытания происходят через равные интервалы времени, так что номер шага служит временным параметром.
. Как обычно, мы считаем, что испытания происходят через равные интервалы времени, так что номер шага служит временным параметром.
Вероятности перехода 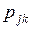 будут расположены в матрицу переходных вероятностей
будут расположены в матрицу переходных вероятностей
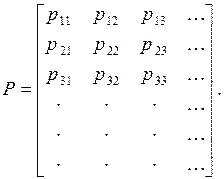 (2)
(2)
где первый индекс означает номер строки, а второй – номер столбца. Ясно, что 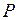 – квадратная матрица с неотрицательными элементами и единичными суммами по строкам. Такая матрица (конечная или бесконечная) называется стохастической матрицей. Любая стохастическая матрица может служить матрицей переходных вероятностей; вместе с нашим начальным распределением
– квадратная матрица с неотрицательными элементами и единичными суммами по строкам. Такая матрица (конечная или бесконечная) называется стохастической матрицей. Любая стохастическая матрица может служить матрицей переходных вероятностей; вместе с нашим начальным распределением 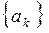 она полностью определяет цепь Маркова с состояниями
она полностью определяет цепь Маркова с состояниями 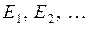 .
.
В некоторых частных случаях бывает удобно нумеровать состояния, начиная с 0, а не с 1. Тогда к матрице 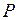 следует добавить нулевые строку и столбец.
следует добавить нулевые строку и столбец.
2. Пояснительные примеры
а) Когда у цепи есть только два возможных состояния 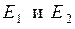 , матрица переходных вероятностей с необходимостью имеет вид
, матрица переходных вероятностей с необходимостью имеет вид
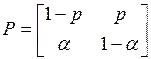 .
.
Подобная цепь могла бы быть реализована в следующем мысленном эксперименте. Частица движется вдоль оси 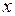 таким образом, что абсолютная величина ее скорости остается постоянной, но направление движения может меняться на противоположное. Говорят, что система находится в состоянии
таким образом, что абсолютная величина ее скорости остается постоянной, но направление движения может меняться на противоположное. Говорят, что система находится в состоянии 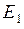 , если частица движется направо, и в состоянии
, если частица движется направо, и в состоянии 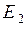 , если она движется налево. Тогда
, если она движется налево. Тогда 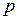 – вероятность поворота, когда частица движется направо, а
– вероятность поворота, когда частица движется направо, а 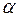 – вероятность поворота при движении налево.
– вероятность поворота при движении налево.
б) Случайное блуждание с поглощающими экранами. Пусть возможными состояниями будут 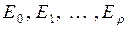 ; рассмотрим матрицу переходных вероятностей
; рассмотрим матрицу переходных вероятностей
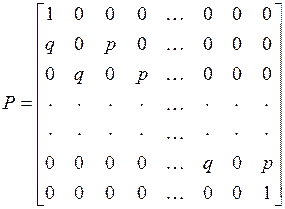 .
.
Из каждого “внутреннего” состояния 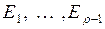 возможны переходы в правое и левое соседние состояния (с вероятностями
возможны переходы в правое и левое соседние состояния (с вероятностями 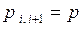 и
и 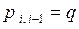 ). Однако ни из
). Однако ни из 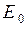 ни из
ни из 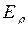 невозможны переходы в какое либо иное состояние; система будет переходить из одного состояния в другое, но коль скоро будет достигнуто
невозможны переходы в какое либо иное состояние; система будет переходить из одного состояния в другое, но коль скоро будет достигнуто 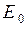 или
или 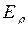 система останется неизменной навсегда.
система останется неизменной навсегда.
в) Отражающие экраны. Интересный вариант предыдущего примера представляет собой цепь с возможными состояниями 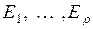 и переходными вероятностями
и переходными вероятностями
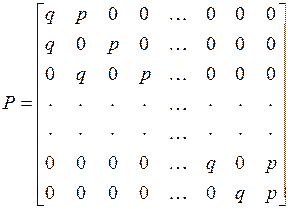 .
.
Эту цепь можно интерпретировать на языке азартных игр, рассматривая двух игроков, ведущих игру с единичными ставками и с соглашением, что каждый раз, когда один из игроков проигрывает свой последний доллар, тот немедленно возвращается ему его противником, так, что игра может продолжаться бесконечно. Мы предполагаем, что игроки вместе имеют 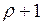 долларов, и мы говорим, что система находится в состоянии
долларов, и мы говорим, что система находится в состоянии 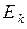 , если их капиталы равны
, если их капиталы равны 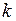 и
и 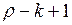 соответственно. Тогда переходные вероятности даются нашей матрицей
соответственно. Тогда переходные вероятности даются нашей матрицей 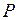 .
.
Дата добавления: 2015-01-19; просмотров: 1566;
