Разложение периодических несинусоидальных кривых в тригонометрический ряд Фурье

Явления, происходящие в линейных цепях при периодических несинусоидальных напряжениях и токах, проще всего поддаются расчету и исследованию, если несинусоидальные кривые раскладывать в тригонометрический ряд Фурье. Из математики известно, что периодическая функция f(ωt), удовлетворяющая условиям Дирихле, т.е. имеющая на всяком конечном интервале времени конечное число разрывов только первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд Фурье

f(ωt)=A_o+ 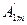sinωt+ 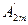sin2ωt+ 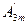sin3ωt+···+ 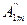cosωt+ 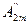cos2ωt+ 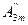cos3ωt+···=

A_o+ .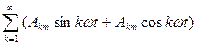

Здесь: Ao – постоянная составляющая или нулевая гармоника; - амплитуда синусной составляющей k-й гармоники; - амплитуда косинусной составляющей k-й гармоники. Они определяются по следующим формулам

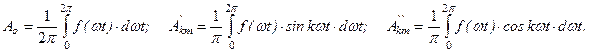
Так как 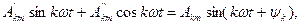где как следует из векторной диаграммы (рис.6.2) 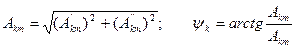, то получаем

.

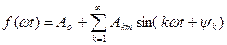Входящие в это выражение слагаемые называются гармониками. Различают четные (k – четное) и нечетные гармоники. Первую гармонику называют основной, а остальные – высшими. Последняя форма ряда Фурье удобна в том случае, когда требуется знать процентное содержание каждой гармоники. Эта же форма ряда Фурье применяется при расчете цепей несинусоидального тока.

Хотя теоретически ряд Фурье содержит бесконечно большое число слагаемых, однако он как правило быстро сходится. а сходящимся рядом можно выразить заданную функцию с любой степенью точности. На практике достаточно взять небольшое число гармоник (3-5) для получения точности расчетов в несколько процентов.