Тема №5. Резонансные явления

Лекция №26. Резонанс напряжений.

Цель: выдать материал про резонанс и условия его возникновения.

Задача: научить определять параметры резонанса.

Резонанс напряжений может возникать в цепях с последовательным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.2.

а)

б)

Рис. 6.2

Общее условие возникновения резонанса напряжений– равенство нулю входного реактивного сопротивления цепи.

Определим условие возникновения резонанса в цепи с последовательным соединением r, L, c (рис. 6.3).

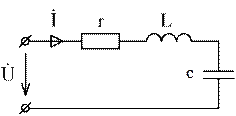
Рис. 6.3

Входное комплексное сопротивление цепи:

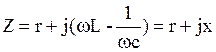. (6.5)

В режиме резонанса входное реактивное сопротивление равно нулю
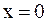( ), и, следовательно,

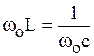. (6.6)

Полученное выражение представляет собой условие возникновения резонанса напряжений в цепи рис. 6.3. В формуле (6.6) величина 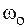– резонансная частота.

Частотные характеристики участка L, c (для цепи рис. 6.3) приведены на рис. 6.4.

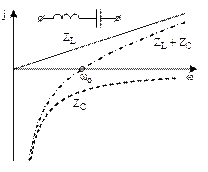
Рис. 6.4

В области частот ниже резонансной ( 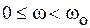) цепь имеет активно-емкостный характер, а в области выше резонансной ( 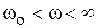) – активно-индуктивный.

Из (6.6) следует, что резонанса можно достичь, изменяя частоту входного напряжения, величину индуктивности или емкости:

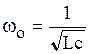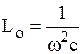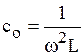, , , (6.7)

где 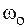, , 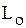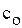– резонансные частота, индуктивность и емкость соответственно.

В режиме резонанса входное сопротивление цепи (рис. 6.3) минимально: 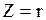, а ток достигает максимального значения:

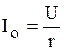. (6.8)

Сопротивление реактивных элементов на резонансной частоте

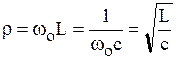(6.9)

называется волновым (характеристическим) сопротивлением резонансного контура.

Отношение

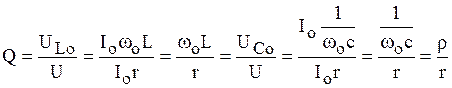(6.10)

называется добротностью резонансного контура.

Добротность показывает, во сколько раз напряжение на реактивных элементах (в режиме резонанса) отличается от входного напряжения. Если при резонансе 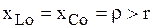и, следовательно, , то напряжение на реактивных элементах (индуктивности и емкости) больше входного напряжения.

Частотные характеристики (зависимости 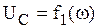, , 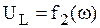, , 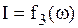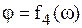) рассматриваемой цепи представлены на рис. 6.5.

Зависимость 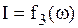получила название резонансной кривой. Чем больше величина добротности контура Q, тем острее резонансная кривая тока (рис. 6.6).

Полоса частот вблизи резонансной, на границах которой ток снижается в 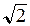от своего максимального значения 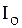, называется полосой пропускания контура. Чем больше добротность Q, тем острее резонансная кривая тока и соответственно меньше полоса пропускания контура (рис. 6.6).

При токе 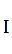, равном 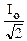, активная мощность рассматриваемой цепи

.

Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине активной мощности 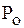, потребляемой цепью при резонансе.

Векторная диаграмма рассматриваемой цепи в режиме резонанса приведена на рис. 6.7.

Рис. 6.5

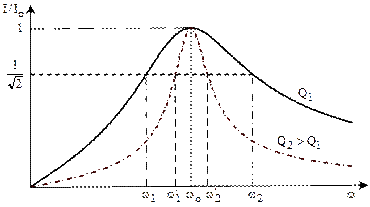
Рис. 6.6

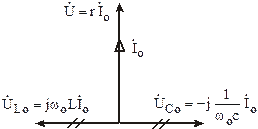
Рис. 6.7